ブリュースター角
カテゴリー:実験物理学
p偏光の光を入射した際に境界面での屈折率の差により、p偏光の反射光強度が、入射角が増すに従って徐々に減少していき一旦0になる(全く反射されなくなる)。
その後、反射光強度は徐々に増していく。
このp偏光の反射光強度が0になる入射角のことをブリュースター角と呼ぶのである。
ブリュースター角の導出
図1のように光が媒質Aから媒質Bに入射する光を考える。
中学で習ったが、光は媒質Aと媒質Bの境界面で一部が反射し、一部が媒質Bに透過する。
どの程度透過し、どの程度反射するかはフレネルの式から導くことができる。
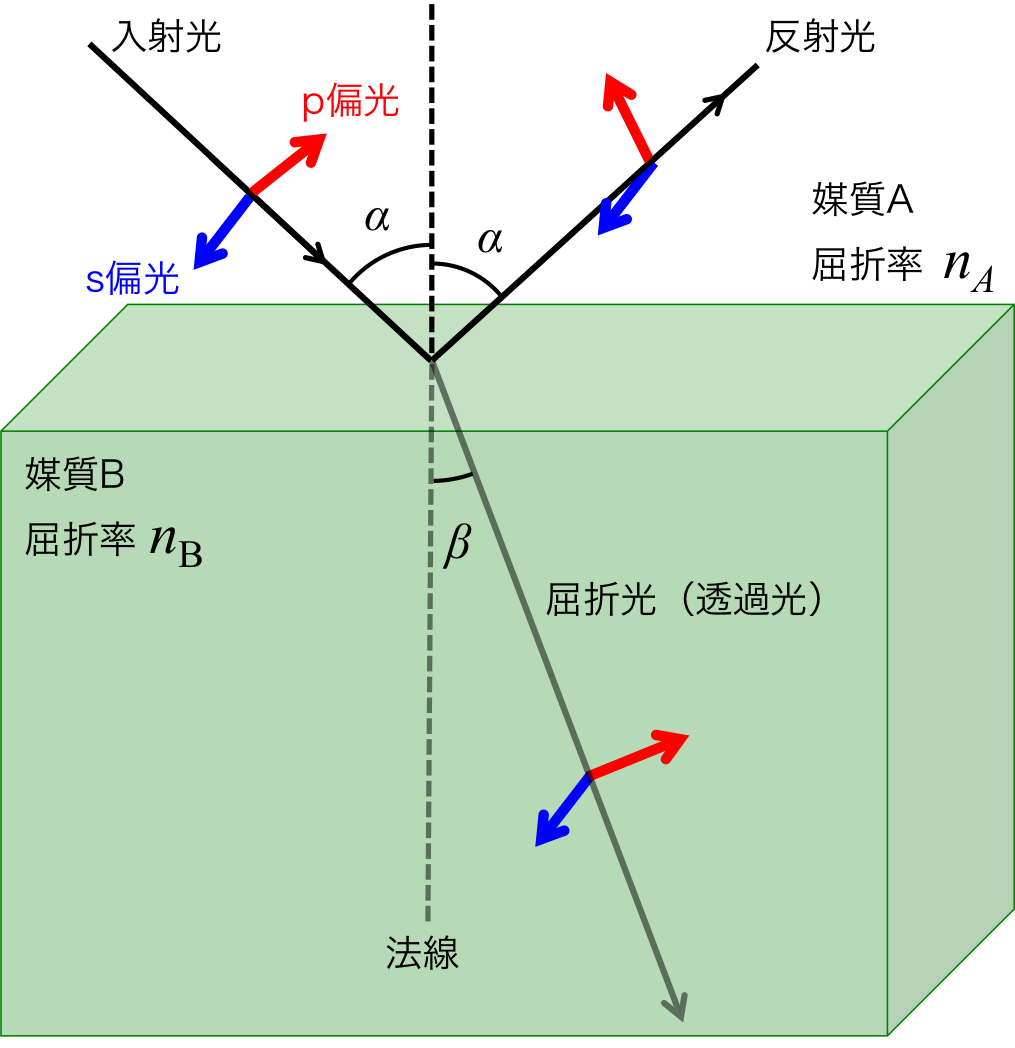
図1. 入射光、反射光、透過光の関係と入射角、反射角、屈折角
フレネルの式を下に示す。(これらの式の求め方は「フレネルの式」のページを参照して欲しい。)
\begin{eqnarray} t_p &=& \frac{2 n_A \cos \alpha}{n_B \cos \alpha + n_A \cos \beta} = \frac{2 \sin \beta \cos \alpha}{\sin(\alpha + \beta)\cos(\alpha - \beta)} \\ r_p &=& \frac{n_B \cos \alpha - n_A \cos \beta}{n_B \cos \alpha + n_A \cos \beta} = \frac{\tan(\alpha - \beta)}{\tan(\alpha + \beta)} \\ t_s &=& \frac{2n_A \cos \alpha}{n_A \cos \alpha + n_B \cos \beta} = \frac{2 \sin \beta \cos \alpha}{\sin(\alpha + \beta)} \\ r_s &=& \frac{n_A \cos \alpha - n_B \cos \beta}{n_A \cos \alpha + n_B \cos \beta} = - \frac{\sin(\alpha - \beta)}{\sin(\alpha + \beta)} \end{eqnarray}
ここで、\( t_p \)、\( r_p \)はp偏光の振幅透過率と振幅反射率で、\( t_s \)、\( r_s \)はs偏光の振幅透過率と振幅反射率である。
透過光強度と反射光強度の関係から、反射光強度は振幅反射率の2乗で表され、透過光強度は振幅透過率に屈折率と入射角、屈折角の余弦を掛け合わせた値になる。
ではp偏光とs偏光の透過光強度\( T_{p,\ s} \)、反射光強度\( R_{p,\ s} \)を具体的に下記に示す。
\begin{eqnarray} T_{p,\ s} &=& \frac{n_B \cos \theta_B}{n_A \cos \theta_A} | t_{p,\ s} | ^2 \\ R_{p,\ s} &=& | r_{p,\ s} | ^2 \end{eqnarray}
ではまず反射光強度から見ていこうと思う。
入射角\( \alpha \)を変化させることで得られる反射光強度を図2に示す。
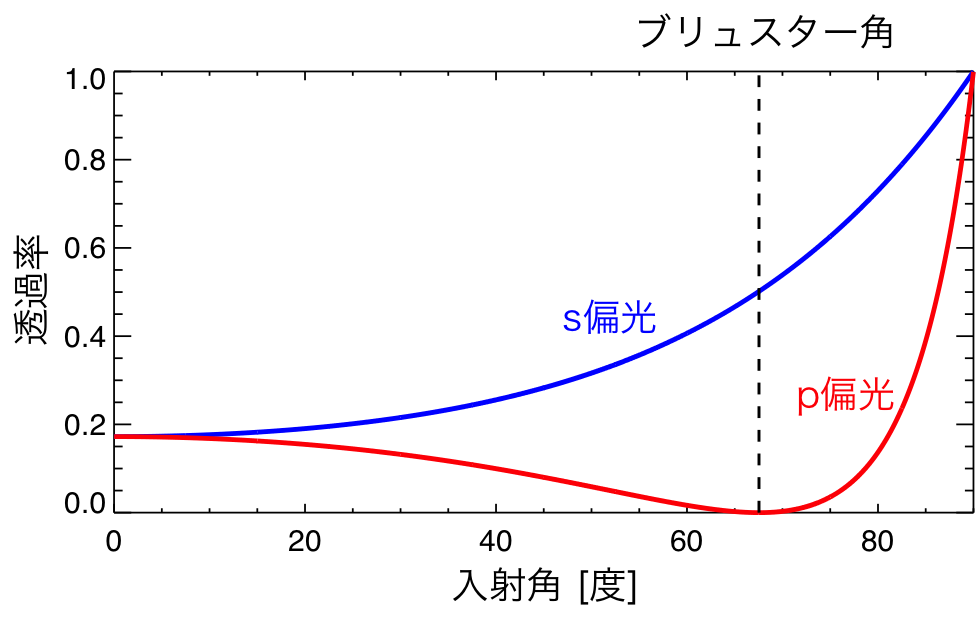
図2. 真空からダイアモンドに入射するp偏光とs偏光の反射光強度
s偏光で入射した光の反射光強度は、入射角\( \alpha \)が大きくなるに従って強くなっていく。
一方、入射したp偏光の光の反射光強度は、入射角\( \alpha \)が大きくなるに従って一旦減少する。
反射率が0になった後は、入射角\( \alpha \)が大きくなるに従って反射光強度は増加する。
この0になる入射角がブリュースター角である。
入射角がブリュースター角\( \alpha_B\)であるとき、反射光と屈折光は直交する。
つまり、\( \beta = 90^{\circ} - \alpha_B \)となる。
フレネルの式の\( r_p \)に0を代入することで、
\begin{eqnarray} \frac{\sin \alpha_B}{\cos \alpha_B} = \tan \alpha_B = \frac{n_B}{n_A} \end{eqnarray}
となるので、ブリュースター角\( \alpha_B \)は、 \begin{eqnarray} \alpha_B = \arctan{\frac{n_B}{n_A}} \end{eqnarray} で表されるのである。
ちなみに透過光強度を見ると、図3のようになる。
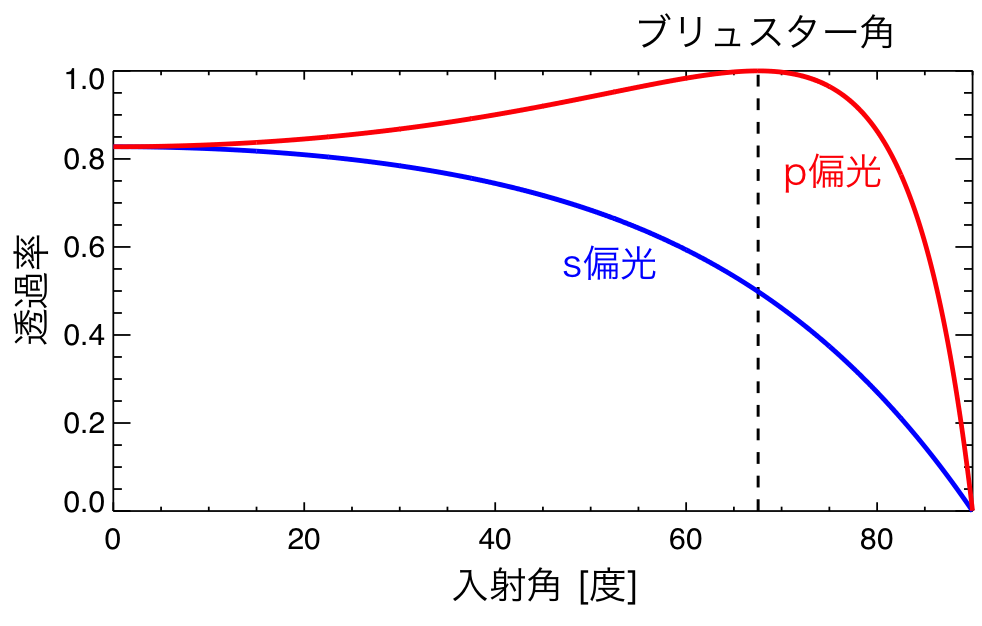
図3. 真空からダイアモンドに入射するp偏光とs偏光の透過光強度
つまり、ブリュースター角で入射したp偏光の光は反射しないので、100%が透過する。
これは、 \begin{eqnarray} T_{p,\ s} + R_{p,\ s} = 1 \end{eqnarray} の法則があるためである。
この性質を使って、反射損失を0にするために実験等で結晶に光を入射させる場合は、入射する光をp偏光にしてからブリュースター角で入射させることが多い。