圧力による仕事

カテゴリー：熱力学

図1のようにピストンのついたシリンダーの内部に物質（例えば気体）を入れて圧縮する場合を考える。ピストンに力を加えていない状態では内部の圧力と外部の圧力が釣り合っている。

ピストンに力を入れて圧縮させると、内部の圧力が外部よりも高くなる。この時、ピストンの圧縮を極めてゆっくり行い内部の熱平衡状態が常に成り立つようにする。

これは準静的過程で、内部の圧力とピストンを押す力が常に釣り合いながら圧縮されていることになる。

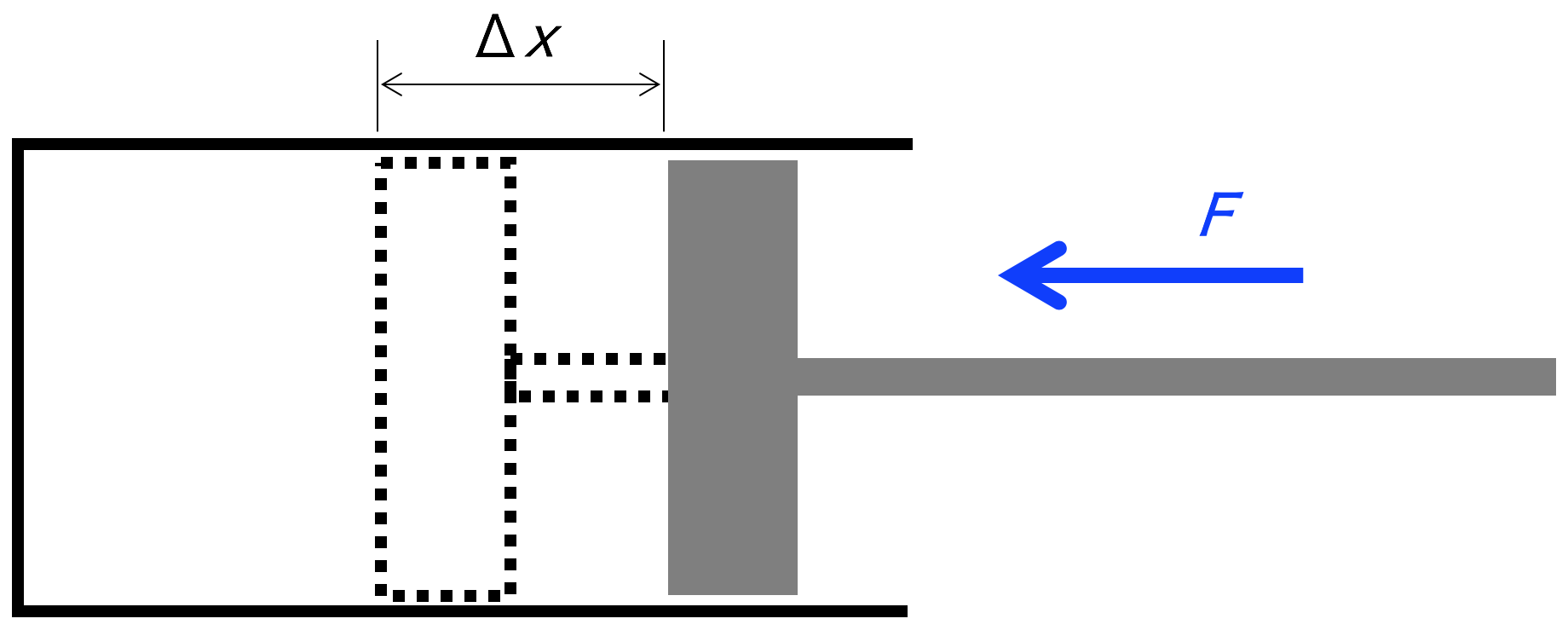
図1. 圧縮による体積変化

ここで、内部の圧力の増加分を\( P \)とすると、この圧力はピストンにかけられた力と釣り合うので

\begin{eqnarray} F = PS \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

となる。ここで、Sはピストンの面積である。また、ピストンが圧縮された時に移動した距離を\( \Delta x \)とするとピストンが物体に対してした仕事は

\begin{eqnarray} \Delta W = F \Delta x = PS \Delta x \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

となる。この時、物体は圧力が上昇する代わりに体積が減少していて、その減少量は

\begin{eqnarray} \Delta V = - S \Delta x \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}

である。式(3)を式(2)に代入することで、

\begin{eqnarray} \Delta W = - P \Delta V \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}

を得るのである。つまり、体積変化を知ることで物体に加えられる、または物体が加える仕事量がわかる。これは、準静的変化であればシリンダーのような考えやすい形の物体である必要はなく、どのような形の物体でも式(3)は成り立つのである。