定圧比熱と定積比熱

カテゴリー：熱力学

定積比熱\( C_V \)と定圧比熱\( C_p \)は以下のように表される。

比熱とは単位質量の物体を1℃（1 K）上昇させるのに必要な熱量のことである。 定積比熱と定圧比熱の違いは、その比熱の測定方法（条件）の違いである。

図1を使って簡単に説明しようと思う。

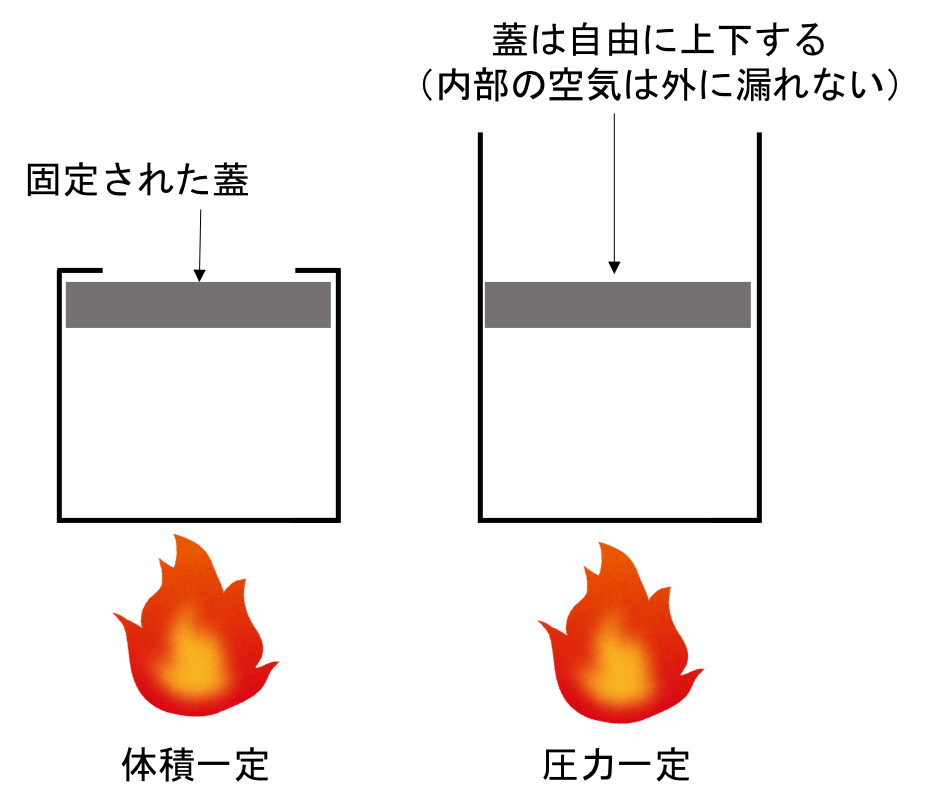
図1. 体積一定と圧力一定での加熱

定積比熱とは体積一定の条件での比熱のことである。

図1の左図のように容器に入れた機体を加熱する際に蓋を固定した場合を考える。 この時、内部の気体を容器ごと加熱する。 すると気体が膨張して蓋を外側に押しやろうとするが、蓋は固定されているため容器の体積は一定に保たれる。 この時、体積変化がないため外部に仕事をしない。 （この詳細は圧力による仕事のページを参考にしてほしい）

つまり、この気体に加えられた熱量がそのまま内部エネルギーの上昇量となる。 この方法で単位質量の物体の温度が1℃上がるために必要な熱量が定積比熱である。

一方で、定圧比熱は右図のように蓋が気体の膨張に合わせて動くようになっている系で計測された比熱である。 気体が膨張すると蓋が上に動くので、容器の内部の圧力は一定に保たれる。 定積比熱の時と異なり、外部に仕事をするために与えられた熱量の全てが内部エネルギーの上昇となるわけではない。

定積比熱と定圧比熱は上記のような違いがあるのである。 上でも説明したが、体積が一定の場合、与えられた熱量がすべて内部エネルギーの上昇となるので、圧力一定の場合と比べて少ない熱量で気体の温度が上昇する。 従って、同じ物体の場合、定積比熱の方が定圧比熱よりも小さくなる。

それぞれの比熱の求め方については、定積比熱の導出方法、定圧比熱の導出方法のページを参考にして欲しい。

また、定積モル比熱、定圧モル比熱という呼び方もある。 この場合は1モルあたりの物体の温度を体積一定、圧力一定の条件で1℃上昇させるのに必要な熱量のことである。