熱力学第１法則

カテゴリー：熱力学

熱力学第1法則と聞くと、

\begin{eqnarray} \Delta U = W + Q \end{eqnarray}

という式を思い浮かべる人が多いと思う。ここで、\( W \)は外部から物質がされた仕事で、\( Q \)は外部から与えられた熱量である。 \( \Delta U \)は加えられた仕事と熱量によって増加した内部エネルギーである。

このページではどのような原理によって上の式が導出されたのか説明する。

図1のようにある基準の状態0からエネルギー\( U_1 \)を与えて状態2にする。そして、状態1に対してエネルギー\( U_2 \)を与えて状態2になった場合を考える。また、もう一つのパターンとして、状態0からエネルギー\( U_3 \)を与えて状態2に一気に移す場合を考える。

この時、

\begin{eqnarray} U_1 + U_2 = U_3 \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

となる。これを熱力学第一法則と呼ぶ。また、もっと力学などで慣れ親しんだ呼び方で呼ぶと、エネルギー保存則と呼ばれる。

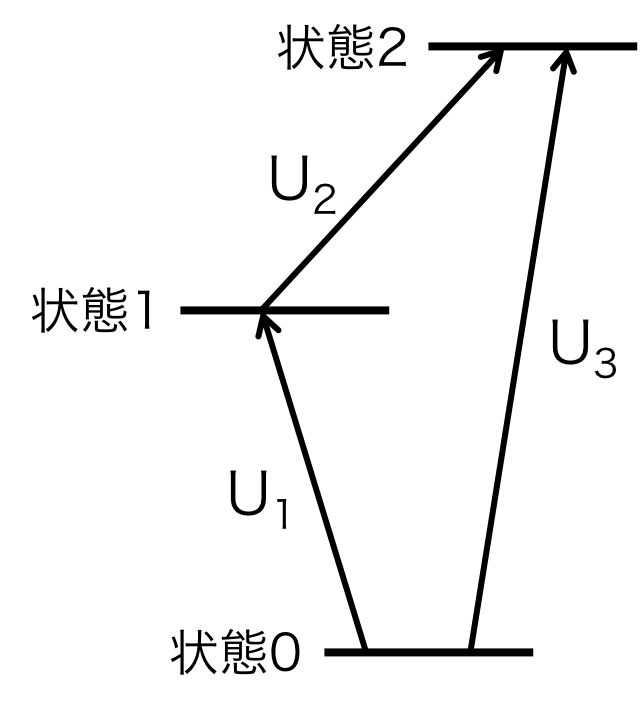
図1. 状態0, 1, 2のエネルギーの関係

物体にエネルギーを与える場合は摩擦を起こして温度を上げることもでき、加熱するなどして熱量を与えることでもできる。また、摩擦と加熱を同時に行っても物体系にエネルギーを貯めることができる。これを踏まえて、式(1)で表された熱力学第１法則を定義すると

１つの物体系を定められた基準の状態から定められた終わりの状態へ様々な方法で移す時、物体系に与えられた力学的仕事と熱量の和は一緒である。

となる。もし、\( U_2 = W + Q \)とすると式(1)は

\begin{eqnarray} U_3 - U_1 = W + Q \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

となる。この式の方がよく使われる形かもしれない。ここで、\( W \)は力学的仕事で物質が外部からされる仕事である。 \( Q \)は熱量である。もちろん、同時に力学的仕事と熱量を加えられるし、片方だけの場合もあり得るので\( Q= 0\)も\( W = 0\)とも成り得るのである。