白色雑音(ホワイトノイズ)
カテゴリー:スペクトル解析
ホワイトノイズ(白色雑音)とはすべての周波数成分の振幅が等しい雑音のことである。
言い換えると、特定の周期で突出した振幅を持たず、すべての周期が平等に同じだけの振幅を持つノイズのことである。
静かな場所で動画を撮っても、入ってしまう「ザー」といった音や、テレビ放送終了後の砂嵐状態や、ラジオなどの「シャー」という音色のないノイズのことを指している。
すべての周波数成分の振幅が等しい時に光の波長に置きかえると、白色に見えると言うことが白色雑音の語源である。
白色雑音(ホワイトノイズ)の特性
様々な計測や数値シミュレーションを行う上でノイズ(雑音)というものの扱いが非常に重要になってくる。
完全な計測というのはほぼ不可能で、必ず計測値にはノイズが含まれる。
またシミュレーションを行う際は、何らかのきっかけが必要である。
その時に、ノイズを初期微動とすることが多いのである。
このノイズの中で最も有名なものが白色雑音(ホワイトノイズ)である。
具体的な白色雑音を図1に示す。
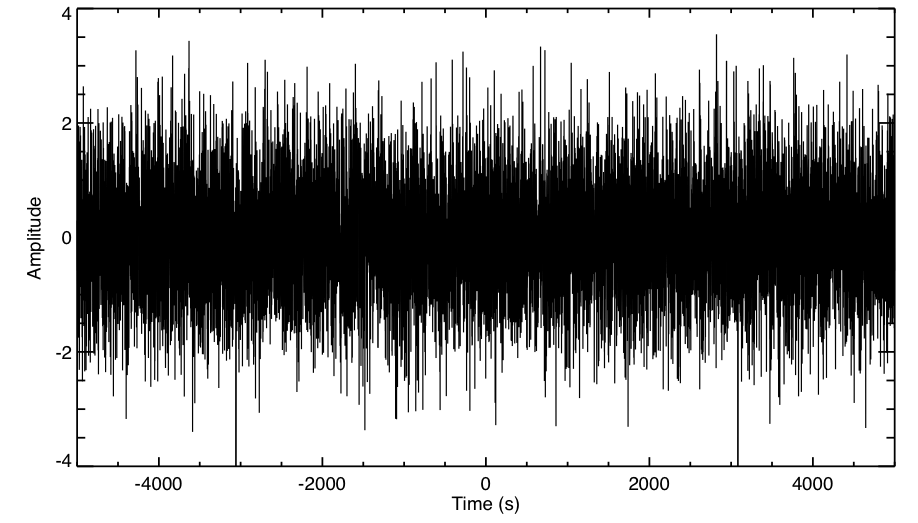
図1. 白色雑音
これを見てわかるように、なんらかの周期で変動しているようには全く見えない。
全てランダムに値が決まっているように見えるが、白色雑音と呼ぶためにはいくつかの特徴を抑えている必要がある。
上で述べた、
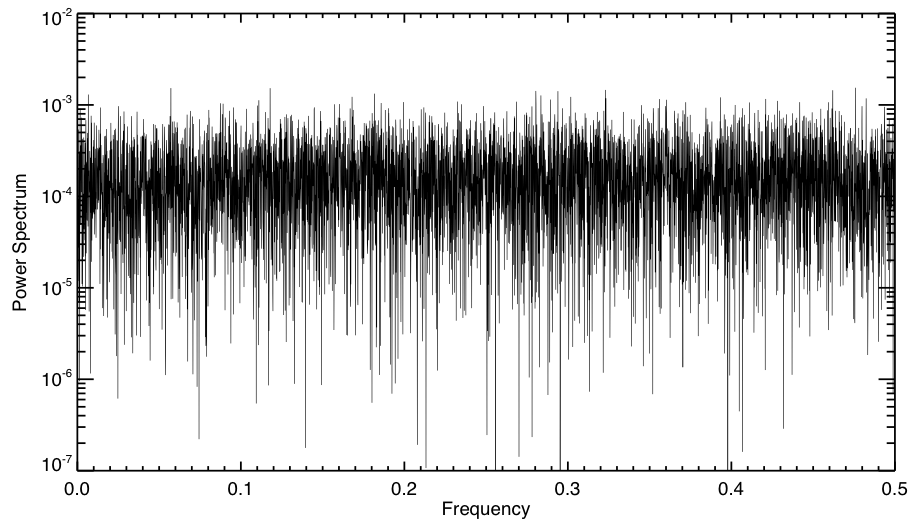
図2. 白色雑音のパワースペクトル
図2に白色雑音のパワースペクトルを示す。
これを見てわかるように、どの周波数であってもほぼ同じパワースペクトルを持っていることがわかる。
これはノイズの中に特出した振幅を持つ周波数成分が存在しないことを示している。
また、ピンク色の光は短周波数から高周波数の強度を見た時に、短周波数のパワースペクトルが強く、高周波数のスペクトルが弱い。
このことから、図3で言えば左肩下がりのパワースペクトルを持つノイズはピンクノイズと呼ばれる。
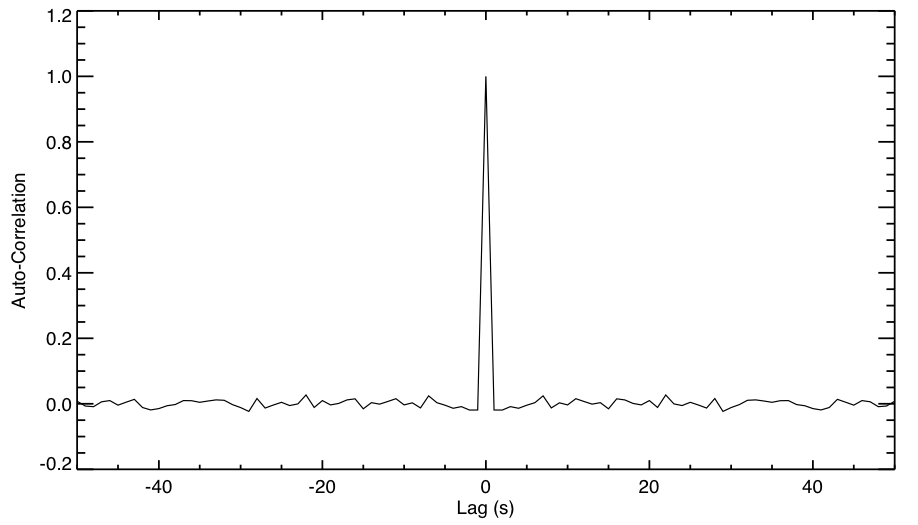
図3. 白色雑音の自己相関関数
教科書などでは、その事が大きく取り上げられているが、実はもう一つ重要な特徴がある。
それは、白色雑音の自己相関関数は、ラグを\( \tau \)とすると、\( \tau=0 \)から離れると急激に0に近づくと言うものである。
実際に図1の白色雑音の自己相関関数を示して見ると図2のようになる。
理想的には\( \tau =0 \)以外で、自己相関関数(図2のy軸)は0になることが望ましいが、そのような理想的なノイズを作り出すことは難しい。