フーリエ級数
カテゴリー:スペクトル解析
フーリエ級数とは、ある関数を三角関数の足し合わせで表現することである。
実際に例を示しながら進めないとわかりにくいので、まずは簡単な例題を示すことから始める。
図1に示すような区間\( ( -T/2, T/2 ) \)を基本とする周期\( T \)を持つ周期関数があったとする。
この周期関数を数式で表すと以下のようになる。
\begin{eqnarray} x(t) = \left\{ \begin{array}{ll} -2 - \frac{4}{T}t & \left( -\frac{3T}{4} < t < - \frac{T}{4} \right) \\ \frac{4}{T}t & \left( -\frac{T}{4} \le t \le \frac{T}{4} \right) \\ 2 - \frac{4}{T}t & \left( \frac{T}{4} < t < \frac{3T}{4} \right) \\ \end{array} \right. \end{eqnarray}
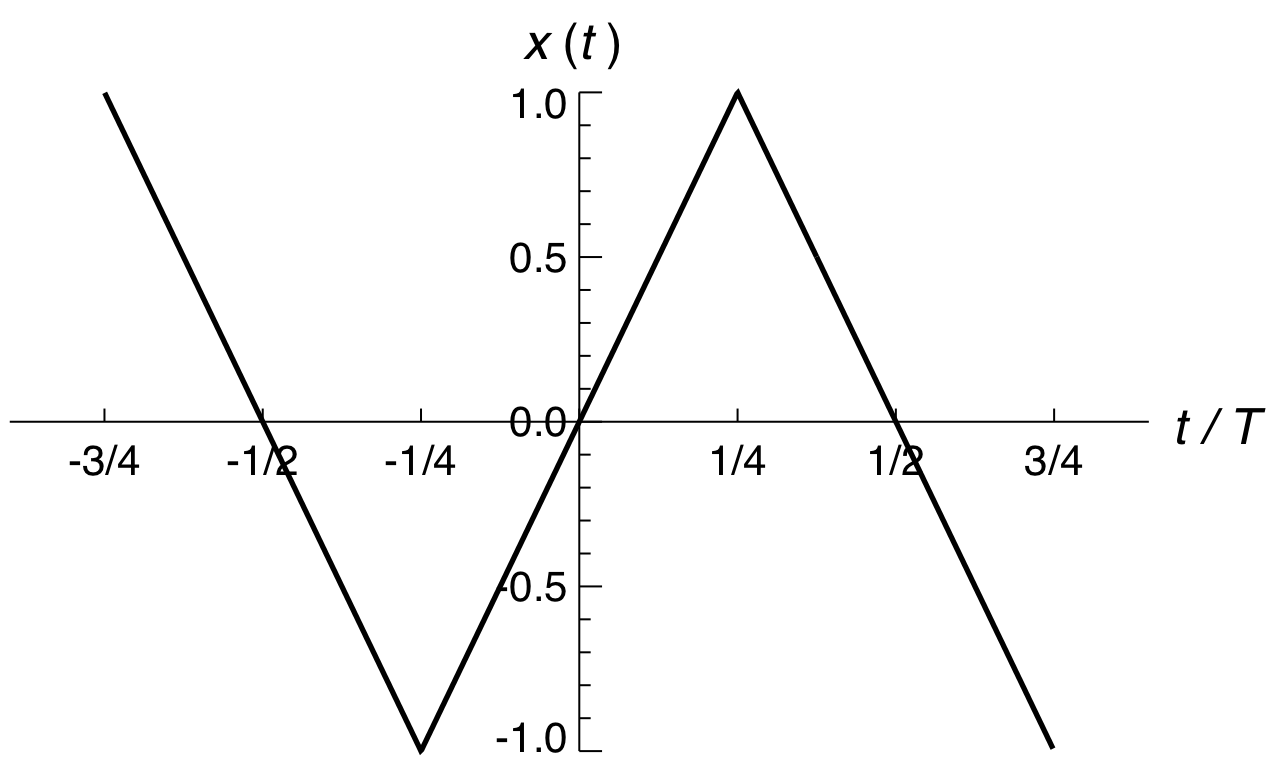
図1.
では、区間\( ( -T/2, T/2 ) \)において、\( x(t) \)を整数個の正弦波の足し合わせで表現できるとする。
この時、\(x(t)\)は奇関数であるから偶関数である余弦波は考えなくていい。
すると、\( x(t) \)は以下のように表わされる。
\begin{eqnarray} x(t) = b_1 \sin \frac{2\pi t}{T} &+& b_2 \sin \frac{4\pi t}{T} + b_3 \sin \frac{6\pi t}{T} \\ + &\cdots& + b_n \sin \frac{2n\pi t}{T} + \cdots \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
ここで、\( b_1,\ b_2,\ b_3,\ \cdots ,\ b_n.\ \cdots \)が未知数であるので、これを求めていく。
式(1)の両辺に\( \sin (2n\pi t/T) \)を掛けて、区間\( ( -T/2, T/2 ) \)で積分をする。
\begin{eqnarray} \int^{T/2}_{-T/2} x(t)\sin \frac{2n\pi}{T}\ dt = b_1 \int^{T/2}_{-T/2} \sin \frac{2\pi t}{T} \sin \frac{2n\pi}{T}\ dt & +& b_2 \int^{T/2}_{-T/2}\sin \frac{4\pi t}{T} \sin \frac{2n\pi}{T}\ dt + b_3 \int^{T/2}_{-T/2} \sin \frac{6\pi t}{T} \sin \frac{2n\pi}{T}\ dt \\ + &\cdots& + b_n \int^{T/2}_{-T/2} \left( \sin \frac{2n\pi t}{T} \right)^2 \ dt + \cdots \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
ここで、右辺と左辺に分けて解いてみる。まず、右辺について考える。
項が多くて積分が大変そうだが、実は1周期にわたる余弦波や正弦波どうしの掛け算の積分は、直交性という性質のため
\( n=m \)の場合を除いて、0になる。つまり、
\begin{eqnarray} \int^{T/2}_{-T/2} \sin \frac{2m \pi t}{T} \sin \frac{2n \pi t}{T}\ dt = \left\{ \begin{array}{ll} &= 0 &(m \ne n) \\ &= \frac{T}{2} &(m = n) \end{array} \right. \ \ (3) \end{eqnarray}
となり、右辺はT/2だけ残ることになる。
では、左辺を計算していく。
\( \sin \)が奇関数であるので、積分区間を\( -T/2 \rightarrow T/2 \)から\( 0 \rightarrow T/2 \)に変化させて、2倍すればいい。
すると以下を得ることができる。
\begin{eqnarray} \int^{T/2}_{-T/2} x(t) \sin \frac{2n\pi t}{T} dt = 2 \left\{ \int^{T/4}_0 \left( \frac{4}{T}t \right) \sin \frac{2n\pi t}{T} dt + \int^{T/2}_{T/4} \left( 2 - \frac{4}{T}t \right) \sin \frac{2n\pi t}{T} dt \right\}\ \ \ \ \ \ \ \ (4) \end{eqnarray}
このままだと積分しづらいので、\( \alpha = \frac{2n\pi t}{T} \)と置くことで以下のように積分を実行することができる。すると、
\begin{eqnarray} = \frac{2T}{(n\pi)^2} \int^{n\pi / 2}_0 \alpha \sin \alpha\ d\alpha - \frac{2T}{(n\pi)^2} \int^{n\pi}_{n\pi /2} \alpha \sin \alpha\ d\alpha + \frac{2T}{n\pi} \int^{n\pi}_{n\pi / 2} \sin \alpha\ d\alpha \\ \\ \left\{ \begin{array}{ll} &= \frac{4T}{(n\pi)^2}(-1)^{(n+1)/2} &(n = 1,3,5, \cdots) \\ &= 0 &(n = 2,4,6, \cdots) \end{array} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
式(5)と式(3)の結果を使うことで、未知数であった\( b_n \)(フーリエ係数)を
\begin{eqnarray} b_n &=& \frac{2}{T} \int^{T/2}_{T/2} x(t) \sin \frac{2n\pi t}{T}dt \\ \\ & &\left\{ \begin{array}{ll} &= \frac{8}{(n\pi)^2}(-1)^{(n+1)/2} &(n = 1,3,5, \cdots) \\ &= 0 &(n = 2,4,6, \cdots) \end{array} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
と得ることができる。よって、\( b_n\)が求まったので、式(1)は以下のようになる。
\begin{eqnarray} x(t) = \frac{8}{\pi} \left\{ \sin \frac{2\pi t}{T} - \frac{1}{3^2}\sin \frac{6\pi t}{T} + \frac{1}{5^2} \sin \frac{10\pi t}{T} - \frac{1}{7^2} \sin \frac{14\pi t}{T} + \cdots \right\}\ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}
この式を実際に図にしてみる。
式(7)の第1項まで、第2項まで、第5項までを図にしたものを図2に示す。
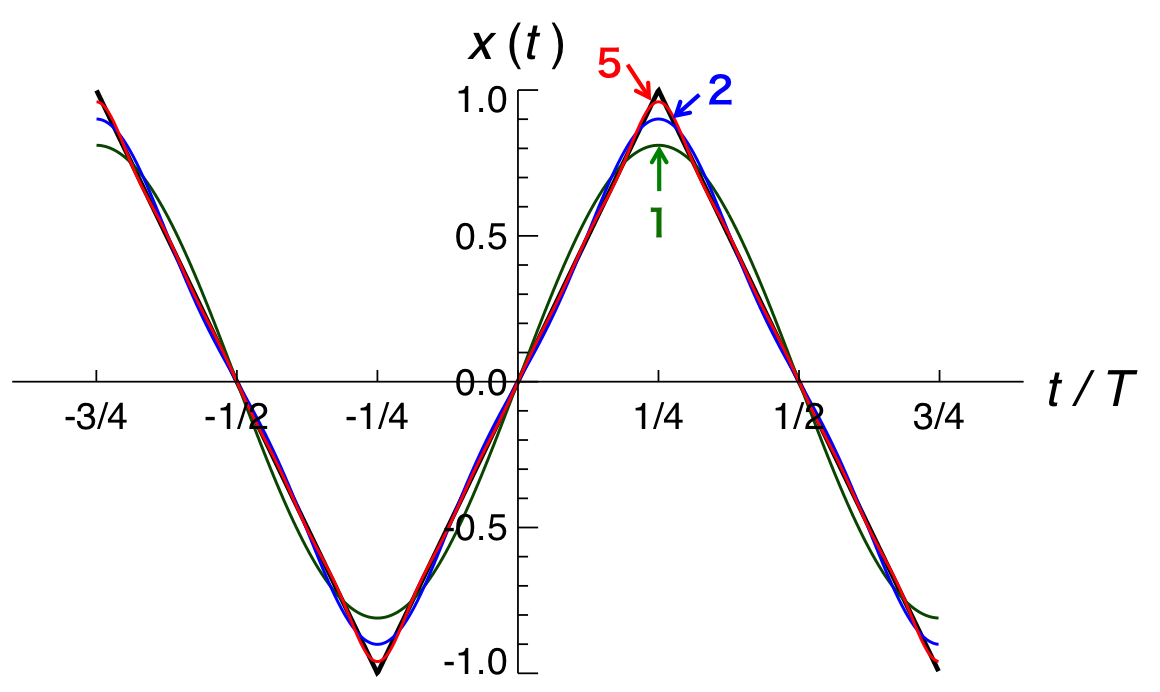
図2.
図2を見てわかるように、第1項だけを表示した場合(緑の線)には、実際の\( x(t) \)の値である黒の三角波はそれほどよく再現はできていない。
第2項まで増やすとかなり再現の精度が上がって来ているように見える。
第5項まで計算すると\( x(t) \)との差分は相当小さくなっていることが伺える。
このように三角関数を含んだ項の足し合わせを多くすればするほど\( x(t) \)に近づいていく。
このようにある関数を三角関数を含んだ項の足し合わせで表現することをフーリエ級数または、 フーリエ級数展開と呼ぶ。
一般的には、区間\( [-T/2,\ T/2] \)を一周期とする周期関数のフーリエ級数は以下のようになる(式(7)と式(7)の余弦の場合で解いた場合を足し合わせたものになる)。
\begin{eqnarray} x(t) &\sim& \frac{a_0}{2} + a_1 \cos \frac{2\pi t}{T} + a_2 \cos \frac{4\pi t}{T} + \cdots + a_n \cos \frac{2n\pi t}{T} + \cdots \\& &\ \ \ \ \ \ b_1 \sin \frac{2\pi t}{T} + b_2 \sin \frac{4\pi t}{T} + \cdots + b_n \sin \frac{2n\pi t}{T} + \cdots \\ &=& \frac{a_0}{2} + \sum_{n=1}^{\infty} \left( a_n \cos \frac{2n\pi t}{T} + b_n \sin \frac{2n\pi t}{T} \right)\ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray}
この時、フーリエ級数\( a_n,\ b_n \)は次のように表される。
\begin{eqnarray} a_n &=& \frac{2}{T} \int^{T/2}_{-T/2} x(t) \cos \frac{2n\pi t}{T}\ dt \ \ \ \ \ \ \ \ \ \ \ \ \ (9) b_n &=& \frac{2}{T} \int^{T/2}_{-T/2} x(t) \sin \frac{2n\pi t}{T}\ dt \ \ \ \ \ \ \ \ \ \ \ \ \ (10) \end{eqnarray}
通常、周期関数をフーリエ級数で正確に表すためには、かなり多くの項を足し合わさなくてはならない。
この項の数は通常は少なくても20から30項を足し合わす必要があるのである。
中高男子必見!【青春のキトー君】