レーダー方程式
カテゴリー:レーダー技術
アンテナから送信された電力はどんどん広がって伝搬していく。
そのためアンテナから遠ければ遠いほど、アンテナから送信された単位面積あたりの電力は小さくなっていく。
目標から再放射されてから受信される電力はさらに小さくなる。
レーダー方程式とは送信した電力、目標の種類、目標までの距離から受信される電力を求めることができる方程式である。
今、無指向性アンテナから電力\( P_t \)の電波が放射された場合を考える。
この電波は、球状に広がっていき、アンテナからの距離が離れれば離れるほど電力密度は低下していく。
つまり、距離\( R \)でのアンテナから送信された電波の電力密度は、
\begin{eqnarray} \frac{P_t}{4 \pi R^2} \ \ \ \ \ \ \ \ (1) \end{eqnarray}
で表される。式(1)の分母はアンテナを中心とする球の表面積を表している。
図1に距離に応じて電力密度が小さくなっていくことを示す。
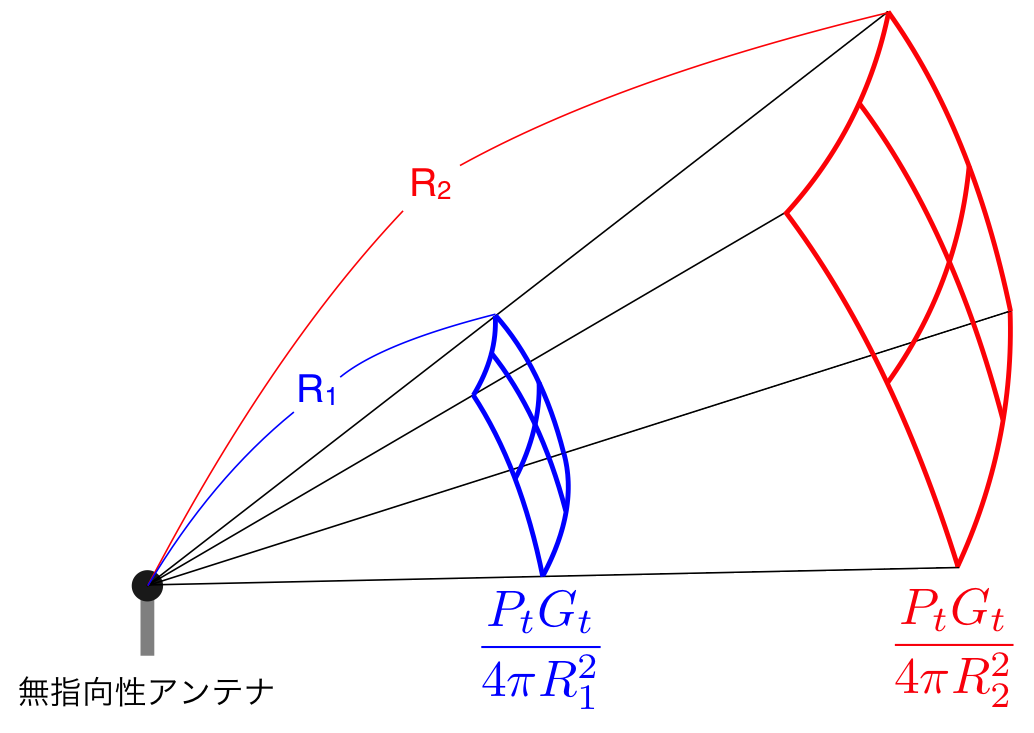
図1. レーダーの送信電力の減衰
この図からも直感的に式(1)がわかると思う。
実際にはレーダーは四方八方に電波を送信しているのではなく、送信する電波を特定の方向に集中されて、高い指向性を実現させているのだ。
この指向性に関係する送信アンテナの電力利得を\( G_t \)とすると、式(1)は書き直すことができて、
\begin{eqnarray} \frac{P_t G_t}{4 \pi R^2} \ \ \ \ \ \ \ \ (2) \end{eqnarray}
となる。目標に電波が当たると反射、または散乱される。
目標がアンテナの方向にどの程度電波を再放射するのかは、面積で表され、それを有効反射断面積と呼ぶ。
有効反射断面積を\( \sigma \)で表すと、目標から再放射される電波の電力密度は、
\begin{eqnarray} \frac{P_t G_t}{4 \pi R^2}\sigma \ \ \ \ \ \ \ \ (3) \end{eqnarray}
と表されるのである。
目標から再放射された電波がアンテナで受信されるので、電波の往復を考える。
つまり式(3)を式(1)の\( P_t \)に代入 すればよくて、受信される電波の電力密度は以下のようになる。
\begin{eqnarray} \frac{P_t G_t}{\left( 4 \pi R^2 \right)^2}\sigma \ \ \ \ \ \ \ \ (4) \end{eqnarray}
この時、送信アンテナと受信アンテナは同じ場所に設置されていると仮定した。
式(4)は電力の密度であるので、最終的にアンテナで受信される電力\( S\)は受信アンテナの有効面積\( A_r \)をかければ良いので、
\begin{eqnarray} S = \frac{P_t G_t \sigma}{\left( 4 \pi R^2 \right)^2}A_r \ \ \ \ \ \ \ \ (5) \end{eqnarray}
である。
ここでは詳しくは述べないが、送信する際の指向性利得\( G_t \)と、受信する際の指向性利得\( G_r \)は以下のように表すことができる。
\begin{eqnarray} G_t &=& \frac{4 \pi A_t}{\lambda^2} \ \ \ \ \ \ \ \ \ (6) \\ G_r &=& \frac{4 \pi A_r}{\lambda^2} \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}
ここで、\( \lambda \)は送信した電波の波長である。
通常のレーダーの場合は送信アンテナと受信アンテナを同一のものにするため、( G_t = G_r = G \)、\( A_t = A_r = A \)とすることができる。
よって、式(5)は
\begin{eqnarray} S = \frac{P_t G^2 \lambda^2 \sigma}{\left( 4 \pi \right)^3 R^4}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray}
で表される。この式こそが、レーダー方程式である。
レーダー方程式を使うことで、目標から返ってくる電波の電力の大きさを計算することができる。
もし、目標までの距離がわかっていれば送信する電力を見積もることができる。
どの程度の受信強度を得られれば良いかの見積もりはそのアンテナの固有のノイズとの比較になる。
これについては、レーダーの最大探査距離のページと、レーダーの最小受信信号のページで説明する。
世界最大級のオンライン学習サイトUdemy