群速度
カテゴリー:プラズマ物理学
一つの式(1)で表される余弦波の伝搬を考える。
\begin{eqnarray} f(x, t) = A_0 \cos (kx - \omega t) \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
ここで、\(A_0\)は振幅、\( k \)は波数、\( \omega \)は周波数である。 図1のように伝搬する余弦波は形を変えないとする。
すると、座標の右側にいる人は余弦波の位相速度で波が伝わって来たということはわかるが、波の振幅が変化しないのでその後は、この波がいつどこで生成されたものなのか変わらない。 簡単に言うと波のエネルギーは振幅の2乗で表されるので、波のエネルギーの変化がないと波の伝搬方向へ情報を伝えることができないのである。 この情報を伝えるために振幅を変化させることを変調と呼ぶ。
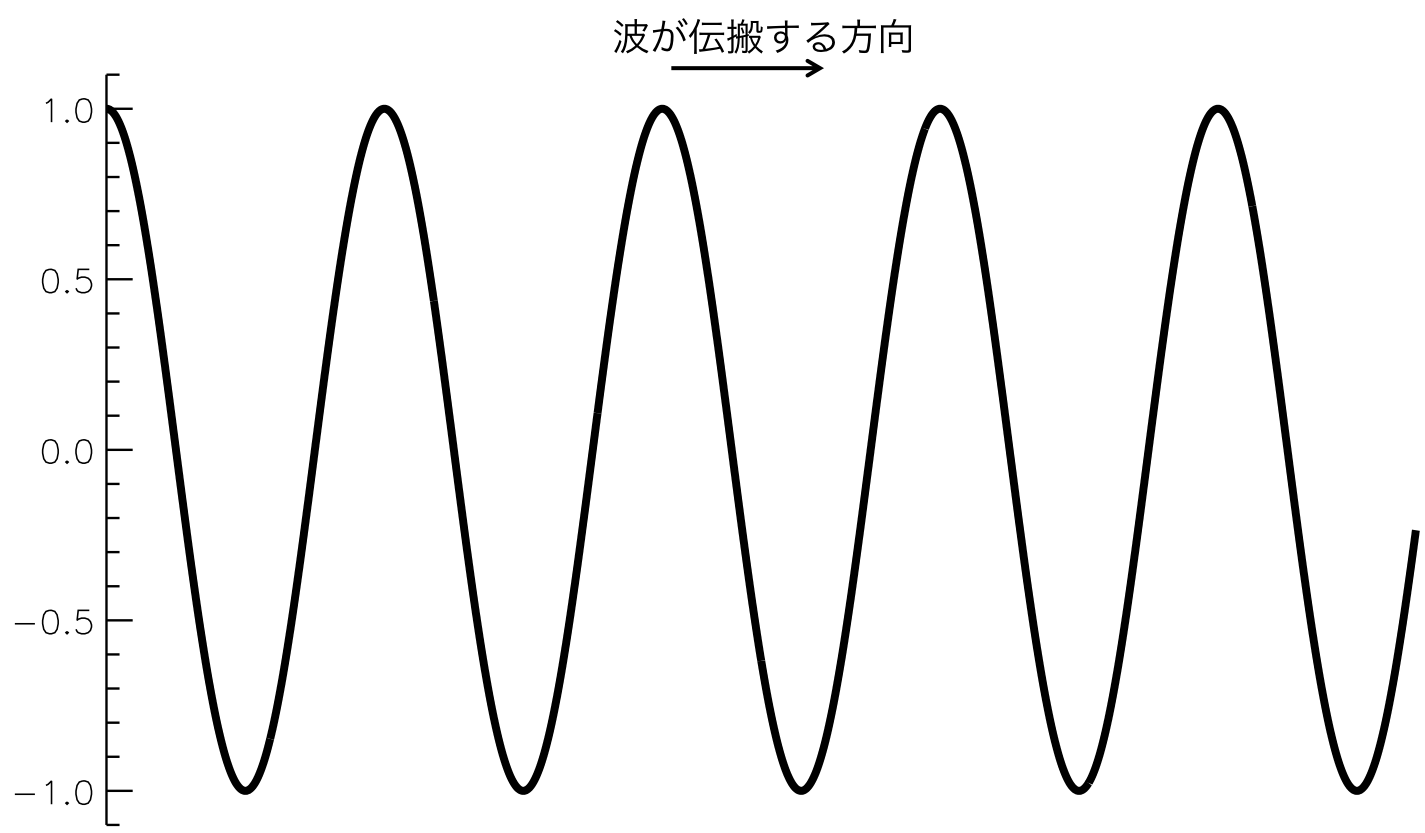
図1. 右方向に伝搬する制限波
変調をするためには、波数と周波数を少しだけずらした波どうしを足し合わせる。 波数と周波数のズレを\( \Delta k \)、\( \Delta \omega \)とすると、2つの波は
\begin{eqnarray} f_1(x, t) = A_0 \cos \{ (k+\Delta k) x - (\omega + \Delta \omega) t\} \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \\ f_2(x, t) = A_0 \cos \{ (k-\Delta k) x - (\omega - \Delta \omega) t\} \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \\ \end{eqnarray}
と表される。 この2つの波動を重ね合わせることをする。 つまり、\( f_1 + f_2 \)とするのである。 2つの波動とその重ね合わせを図で示すと図2のようになる。
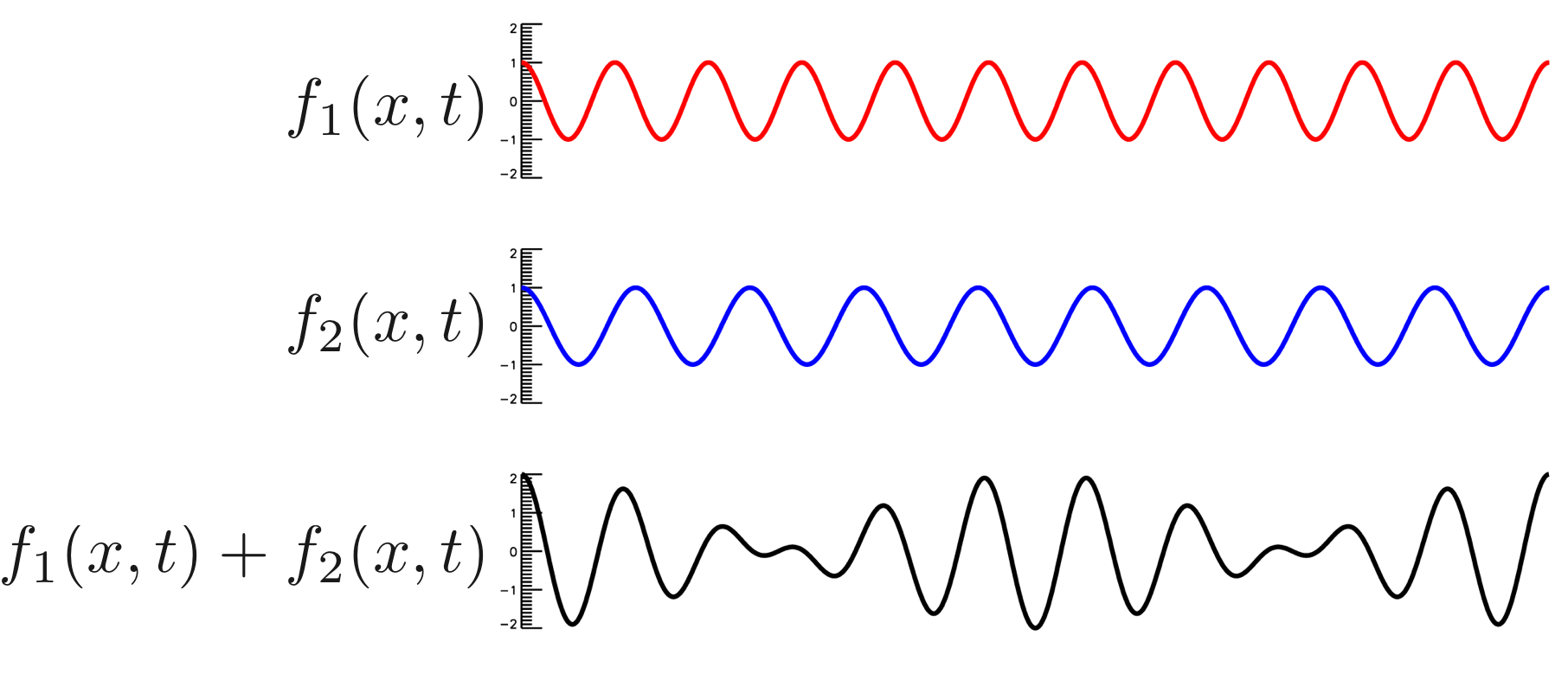
図2. うなりの発生
一番下のプロットを見てもらうとわかるように、少し波数と周波数をずらした波動を足し合わせると、振幅が周期的に振動する波動が作りださせる。 この波動のことを「うなり」と呼ぶ。 このように、波数と周波数を少しずらした波動を足し合わせることで振幅を変化させる変調を起こすことができ、情報を運べるようになるのである。 この方式はAMラジオで用いられている。 では、この変調にはどのような特徴があるか見て行こうと思う。
まず
\begin{eqnarray} a &=& kx - \omega t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)\\ b &=& \Delta k x - \Delta \omega t \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
と置くと、\( f_1 + f_2\)は
\begin{eqnarray} f_1(x,t) + f_2(x,t) = A_0 \cos(a - b) + A_0 \cos(a + b)\ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
と簡単に表される。 これを三角関数の加法定理を使って展開すると
\begin{eqnarray} f_1(x,t) + f_2(x,t) &=& A_0 ( \cos a \cos b + \sin a \sin b + \cos a \cos b - \sin a \sin b ) \\ &=& 2A_0 \cos a \cos b \\ &=& 2A_0 \cos(\Delta k x - \Delta \omega t ) \cos( k x - \omega t ) \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}
となることがわかる。 つまり、式(1)で示された波動に対して\( \Delta k,\ \Delta \omega \)だけずらした波動を足し合わせると、 式(1)の波動の振幅を\( \cos(\Delta k x - \Delta \omega t ) \)で変調させることになるのである。 つまり、図3のようになる。
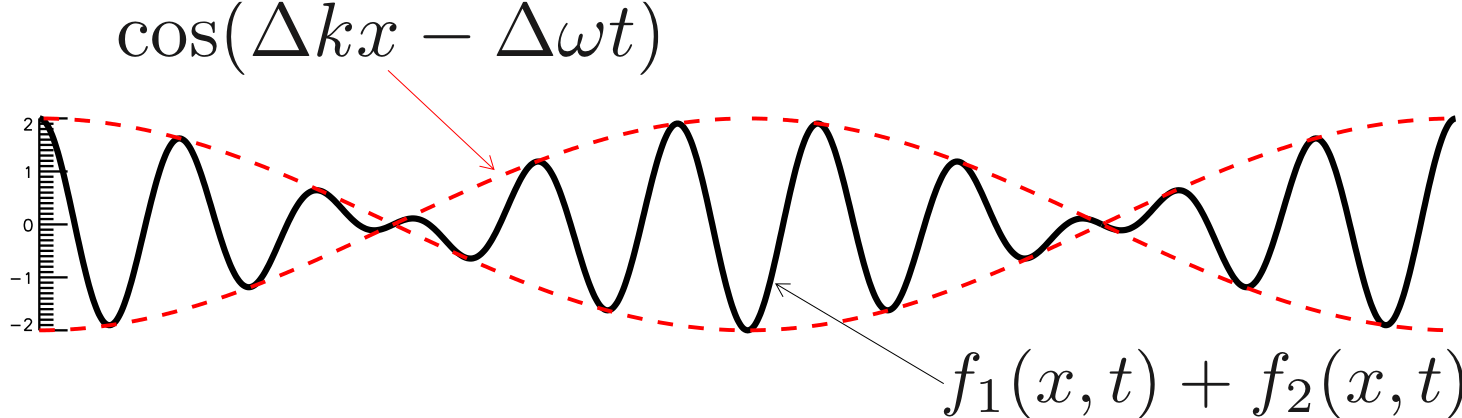
図3. うなりと波束
赤の点線で示される\( \cos(\Delta k x - \Delta \omega t ) \)で囲まれた中に変調された波動が入っていることがわかる。 これは波が束になっているように見えることから波束と呼ばれる。 この波束が伝搬していく速度のことを群速度と呼ぶのである。
従って、群速度\( v_g \)は位相速度を求めた際と同様にして
\begin{eqnarray} v_g = \frac{\Delta \omega}{\Delta k}\ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray}
と表されるのである。ここで、\( \Delta \omega \rightarrow 0 \)の極限を取ることで、群速度は
\begin{eqnarray} v_g = \frac{d \omega}{d k}\ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray}
と書き換えられるのである。 式(8)を使って群速度は通常求められる。