移流

温度や密度などが空間的にばらつきを持って存在している場合を考える。このとき、温度や密度が移動することで1地点で観測している観測者には見かけ上温度や密度が変化したように見える。この効果のことを移流と呼ぶ。

具体的な例を出して移流を考えてみたいと思う。図1のように地点\( x_A \)、\( x_B \)の上空に温度\( T_A,\ T_B\)の空気塊（くうきかい）A, Bがあるとする。

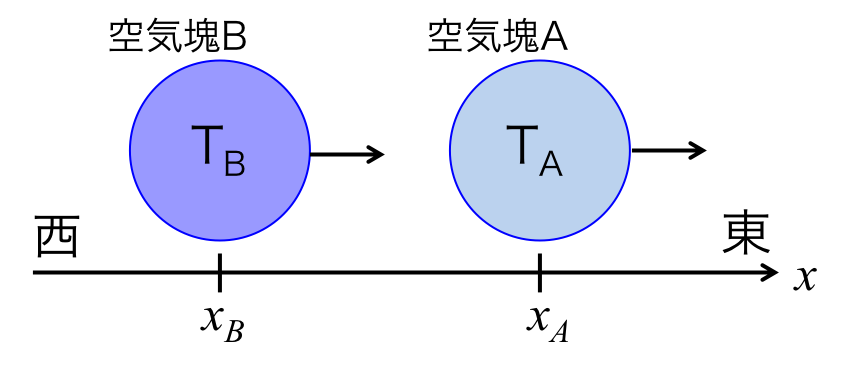
図1.　空気塊の移動

この時、\( T_A > T_B \)で\(T_B\)の方が冷たい空気であるとする。今、西から東に向かって風が吹いていて空気塊もこの風によって流される。するといつしか、空気塊Bはは\( x_A \)の地点に来る。

もし、観測者が\( x_A \)の地点に居たとしたら、時間が立つと温度が下がったように感じる。しかし、別の考え方だと、空気塊の温度は変化していないが、温度が異なる空気塊が移動してきたことによって温度が下がったと考えることもできる。この時、前者のようなある１地点での時間変化だけを考えることをオイラー的と言う。

一方で、移動してきた空気塊によって温度が下がったという空間的に考えることをラグランジュ的という。

繰り返しになるが、移流とはラグランジュ的な考え方の時に現れる効果で、温度や密度のばらつきが移動することによって1地点での温度や密度が変わったように見えるという意味なのである。

次に数学的に移流とはなにか考えていく。ここでは上の例に従って温度変化で考えていく。もし1地点における温度変化を計算したかったら

\begin{eqnarray} \frac{\partial}{\partial t} T\ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

と表される。では、温度の全微分はどのように表されるのであろうか？対流微分のページでも示したように、温度の全微分は

\begin{eqnarray} \frac{d}{dt} T = \frac{\partial T}{\partial t} + \left( {\bf u} \cdot \nabla \right) T\ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

と表されるのである。この時、\( {\bf u} \)は、ある物理量の速度であり、この場合は空気塊の速度のことを意味する。さきほど示したように右辺の第1項はある地点での温度変化である。

第2項はいったい何を示すのであろうか？この第2項こそが移流を表しており、ある注目する物理量が移動することによる変化量のことを示しているのである。上の例で例えると空気塊が移動することによる変化なのである。このことから、式(1)はオイラー（Euler）微分、式(2)はラグランジュ（Lagrange）微分と呼ばれることもある。

もう少し踏み込んで考えてみよう。図1で示した空気塊の移動の問題では、空気塊自体はその内部の温度を変化させていない。つまり

\begin{eqnarray} \frac{d}{dt} T = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}

であり、式(2)の左辺は０となる。つまり

\begin{eqnarray} \frac{\partial T}{\partial t} = - \left( {\bf u} \cdot \nabla \right) T\ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

となり、地点\( x_A \)上空での温度の時間変化は全て移流によるものであったことがわかるのである。つまり、オイラー的とは、ある1地点での変化を考えているものであり、ラグランジュ的とはその物理量の移動を追いかけながらその変化を考えていると言えるのである。

上の例で言えば、地点\( x_A \)でずっと温度観測しているのがオイラー的で、飛行船などに乗って空気塊とともに移動しながら空気塊\( A \)の温度変化をずっと観測しているのがラグランジュ的というわけである。この考え方は物理学（特に気象や大気物理）では極めて重要な考え方であるので覚えておいたほうがいい。