反磁性ドリフト
カテゴリー:プラズマ物理学
磁場中にプラズマが存在すると、プラズマ中の電子とイオンは旋回運動をする。 磁場に加えて電場が存在すると、プラズマ中の電子とイオンはE×Bドリフトをする。 このように磁場と電場の存在によって運動が大きく変わるプラズマであるが、プラズマ自身に密度勾配がある場合はさらに面白い振る舞いを見せるのである。
これは反磁性ドリフトと呼ばれ、電子とイオンの旋回中心は変化しないのではあるが、もっと巨視的(電子やイオンが判別できないくらい離れて見る) とプラズマの塊としてドリフトしているように見える現象が起こる。
つまり、電子とイオンは同じ場所を旋回しているだけなのに、プラズマが全体的にドリフトして見えるということである。 このような奇妙な現象についてこのページでは説明していこうと思う。
プラズマの各粒子に対する運動方程式は
\begin{eqnarray} mn \left\{ \frac{\partial {\bf v}}{\partial t} + ({\bf v}\cdot \nabla){\bf v} \right\} = qn ({\bf E} + {\bf v}\times {\bf B}) - \nabla p\ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
となる。
密度勾配は状態方程式からもわかるように圧力勾配の項にその効果が含まれている。 ここで、\( v_{\perp}\)のみを考え、\( v_{\perp}\)は以下のように正弦的に振動すると仮定して各項の大きさについて考えていく。
\begin{eqnarray} v_{\perp} = v_{\perp} e^{ \left\{ i({\bf k}\cdot{\bf r} - \omega t)\right\} } \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
まず、式(2)のように置くことで、速度の時間微分\( \partial / \partial t \)は\( - i \omega \)とすることができる。 次に式(1)の\( \partial {\bf v} / \partial t\)と\( {\bf v}\times {\bf B} \)を比較するためにこの2つの項を割る。
\begin{eqnarray} \left| \frac{\frac{\partial {\bf v}}{\partial t}}{{\bf v}\times {\bf B}} \right| = \left| \frac{mni\omega v_{\perp}}{q n v_{\perp} B} \right| \sim \frac{\omega}{\omega_c}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
ここで、\( \omega_c\)は粒子のサイクロトロン周波数(ジャイロ周波数)である。
このことから、サイクロトロン周波数\( \omega_c\)に対して十分ゆっくりな振動の\( \omega \)に対しては式(3)はほぼ0となる。 つまり、式(1)の第1項は無視することができる。 後で示されるが、反磁性ドリフトは\( ({\bf v}\cdot \nabla){\bf v} \)に対して垂直であるのでこの項も無視することができる。 従って、式(1)の左辺は無視することができて
\begin{eqnarray} 0 = qn ({\bf E} + {\bf v}\times {\bf B}) - \nabla p\ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}
とすることができる。 この式の右側から\( {\bf B} \)を掛けることで
\begin{eqnarray} 0 &=& qn ({\bf E}\times {\bf B} + {\bf v}\times {\bf B} \times {\bf B}) - \nabla p \times {\bf B} \\ &=& qn ({\bf E}\times {\bf B} - v_{\perp} B^2) - \nabla p \times {\bf B}\ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
となる。 つまり
\begin{eqnarray} v_{\perp} = \frac{{\bf E}\times {\bf B} }{B^2} - \frac{\nabla p \times {\bf B}}{qnB^2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
を得る。 この時、第1項は電場と磁場によるExBドリフト\( v_{E} \)で、第2項が反磁性ドリフト\( v_{D} \)である。
\begin{eqnarray} v_{E} &=& \frac{{\bf E}\times {\bf B} }{B^2} \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \\ v_{D} &=& \frac{\nabla p \times {\bf B}}{qnB^2} \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray}
上で示したようにプラズマの個々の粒子のドリフトではなく、粒子は固定されているがプラズマ全体としてはある1方向にドリフトしているというのが反磁性ドリフトである。 これは一体どういうことなのか、簡単に説明しておく。
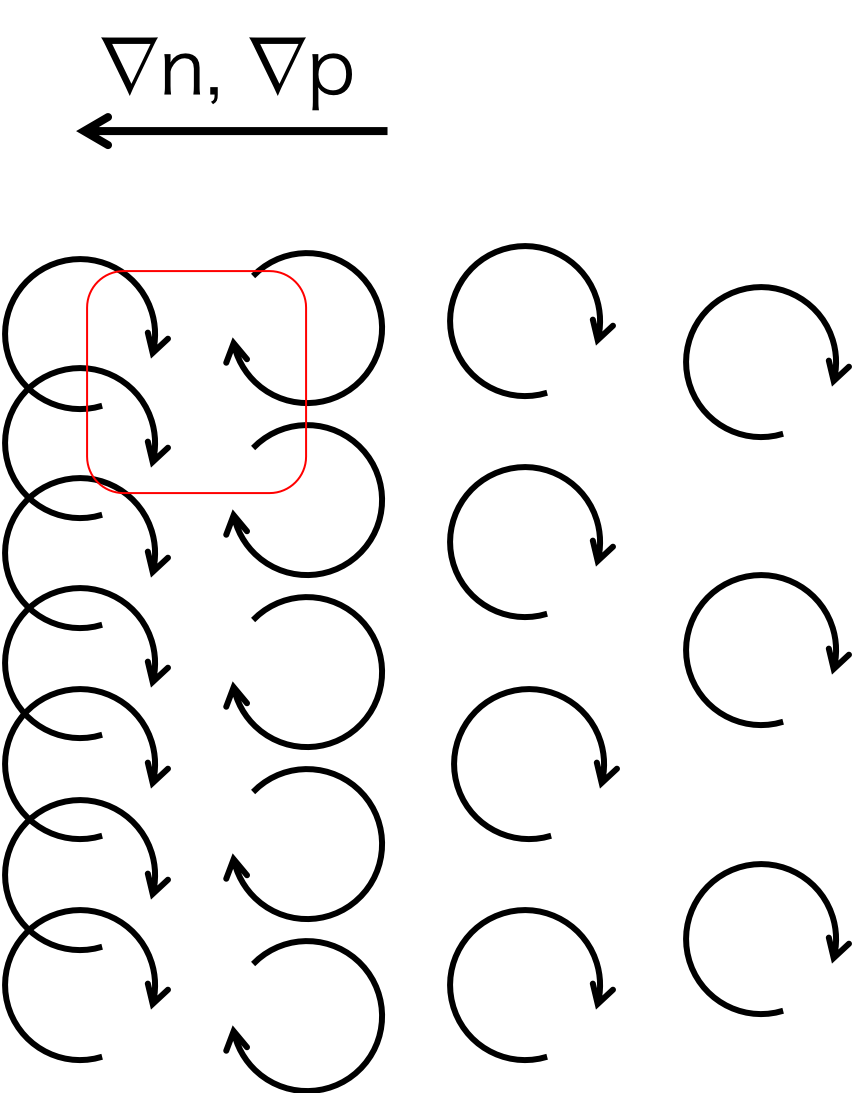
図1. 密度(圧力)に勾配がある場合のプラズマの運動。左方向であるほど密度と圧力が大きい。
プラズマに密度勾配があり、そこに磁場があると個々の粒子は回転運動を始める。 図1に示したように密度勾配が左向きにあると左側では回転している粒子が多くなる。
ここで、図1の赤の四角で囲った部分に注目する。 この四角内部では下向きに進む粒子が2つで上向きに進む粒子が1つだけである。 このことから正味の粒子の運動は下向きとなる。 従って、プラズマは全体的に見ると下向きにドリフトしているように見えるのである。 これが反磁性ドリフトである。
反磁性ドリフトは電荷によって方向が異なる。 つまり電子と正電荷ではドリフト方向が真逆になるので、電流が生じる。 この電流は反磁性電流と呼ばれ
\begin{eqnarray} {\bf j}_D = ne({\bf v}_{Di} - {\bf v}_{De}) = ( k_B T_i + k_B T_e ) \frac{{\bf B} \times \nabla n }{ B^2 } \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray}
と表される。