非一様電場中の運動
カテゴリー:プラズマ物理学
図1のように電場が\(x\)方向にかけられており、強さが\( y \)方向に沿ってその大きさが正弦波的に変化する系の中でのプラズマの運動を考える。 ここで、磁場は一様である。 この電場は
\begin{eqnarray} {\bf E}(y) = E_0 (\cos ky) \hat{\bf x}\ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
で分布するものとする。ここで、\( k \)は波数で、波長\( \lambda \)と\( \lambda = 2 \pi / k \)の関係がある。 このような場合は電荷分布に非一様が生まれた場合に生じ、実際にはプラズマ中に波が伝搬する場合によって生じた電荷分布の非一様によって正弦波的な電場が形成される。
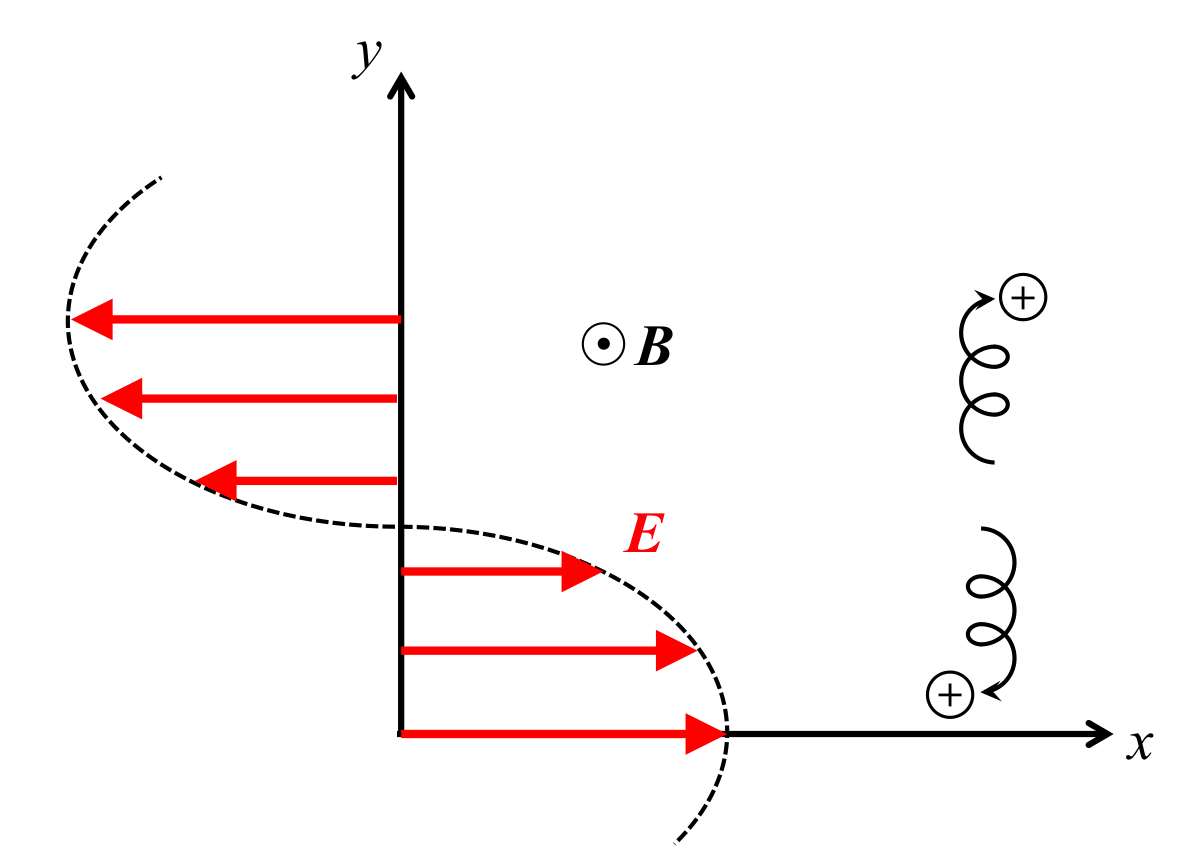
図1. 変化する電場中の正電荷に帯電したプラズマの運動
では、この正弦波的に変化する電場によってどのようなプラズマの運動が生じるのか見ていこうと思う。 プラズマの運動方程式は
\begin{eqnarray} m \frac{d {\bf v}}{dt} = q \left( {\bf E}(y) + {\bf v} \times {\bf B} \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
となる。ベクトルの外積を計算して、磁場に垂直な成分は以下のように表される。
\begin{align} \dot{v}_x &= \frac{qB}{m} v_y + \frac{q}{m} E(y) &(3)\\ \dot{v}_y &= - \frac{qB}{m} v_x &(4) \end{align}
この式(3), (4)を時間微分すると
\begin{align} \ddot{v}_x &= \frac{qB}{m} \dot{v_y} &(5)\\ \ddot{v}_y &= - \frac{qB}{m} \dot{v}_x &(6) \end{align}
となる。式(3), (4)を式(5), (6)に代入すると、以下を得る。
\begin{align} \ddot{v}_x &= - \omega^2 v_{x} &(7) \\ \ddot{v}_y &= - \omega^2 v_{y} - \omega^2 \frac{E(y)}{B} &(8) \end{align}
この方程式は粒子一つ一つの運動を見ている(旋回中心の運動ではない)。 ここで、\( \omega \)はプラズマの旋回(ジャイロ)周波数で、
\begin{eqnarray} \omega = \frac{|q|B}{m} &(9) \end{eqnarray}
で与えられる。 \( E(y) \)はプラズマ粒子の\( y\)座標によって決まるので、プラズマ粒子は回転運動を1周期行う間に異なる強さの電場から力を受けるのである。 では、この電場がプラズマの運動に与える影響を評価していこうと思う。
まずは、\( E(y) \)の振幅が非常に小さいと仮定すると、プラズマが電場がない場合と同様な軌道を取ると近似することができる。 一様な磁場中のプラズマの運動の\( y \)座標の変化は
\begin{eqnarray} y = y_0 \pm r_L \cos \omega t \ \ \ \ \ \ \ \ \ \ \ (10) \end{eqnarray}
で表される。ここで、\(y_0\)は旋回中心の\(y\)座標であり、\( r_L \)はラーモア半径で
\begin{eqnarray} r_L = \frac{m v_{\perp}}{|q|B}\ \ \ \ \ \ \ \ \ \ \ (11) \end{eqnarray}
である。式(1)、(8), (10)から以下の式を導くことができる。
\begin{eqnarray} \ddot{v}_y = - \omega^2 v_y - \omega^2 \frac{E_0}{B} \cos k \left( y_0 \pm r_L \cos \omega t \right)\ \ \ \ \ \ \ \ \ \ \ (12) \end{eqnarray}
ここで、非一様な電場によって、プラズマがどのような運動をさせられるか少し予想する。 非一様ではなく、一様な電場と磁場中のプラズマの運動は、円運動しながら旋回中心が\( {\bf E} \times {\bf B} \)方向にドリフトする。 つまり、非一様な電場によってもプラズマはおそらく旋回中心がドリフトするものと考えられる。
よって、次の操作では式(12)の回転運動を1周期にわたって平均することで、旋回中心の運動を導出する。 式(12)式の\( \ddot{v}_y \)は円運動を与えるための加速度で1周期にわたって平均することで、0となる。 つまり、\( \overline{\ddot{v}_y} =0\)となる。 よって、1周期平均された式(12)は
\begin{eqnarray} 0 = - \omega^2 \overline{v}_y - \omega^2 \frac{E_0}{B} \overline{\cos k \left( y_0 \pm r_L \cos \omega t \right)}\ \ \ \ \ \ \ \ \ \ \ (13) \end{eqnarray}
となるのである。\( \overline{v}_y \)は旋回中心の\( y \)方向の速度である。 \( \cos \)の項がどのような値を取るのかこれだけでは不明なので、もう少し分かりやすい形に変化させていく。 \( \cos \)の項を加法定理を使って展開すると
\begin{eqnarray} \cos k \left( y_0 \pm r_L \cos \omega t \right) = \cos (ky_0) \cos(k r_L \cos \omega t) \mp \sin (ky_0) \sin(k r_L \cos \omega t)\ \ \ \ \ \ \ \ \ \ \ (14) \end{eqnarray}
となる。ここで、ラーモア半径\( r_L \)は非常に小さい(\(<<1\))ので、\(k r_L << 1\)である。 よって、\( \cos (k r_L ) \)、\( \sin (k r_L ) \)はテイラー展開を使って以下のように近似することができる。
\begin{align} \cos (k r_L \cos \omega t) &\approx 1 - \frac{1}{2} \left( k r_L \cos \omega t \right)^2 &(15) \\ \sin (k r_L \cos \omega t) &\approx k r_L \cos \omega t &(16) \end{align}
式(14)は、式(15), (16)を使って
\begin{eqnarray} \cos k \left( y_0 \pm r_L \cos \omega t \right) \approx \cos (ky_0) \left( 1 - \frac{1}{2} \left( k r_L \cos \omega t \right)^2 \right) \mp \sin (ky_0)k r_L \cos \omega t\ \ \ \ \ \ \ \ \ \ (17) \end{eqnarray}
と近似できるのである。 式(17)をプラズマの円運動の1周期\( T \)で平均を取る。 分かりやすいように、\( \cos \omega t\)、\( \cos^2 \omega t \)の時間変化を図2に示す。
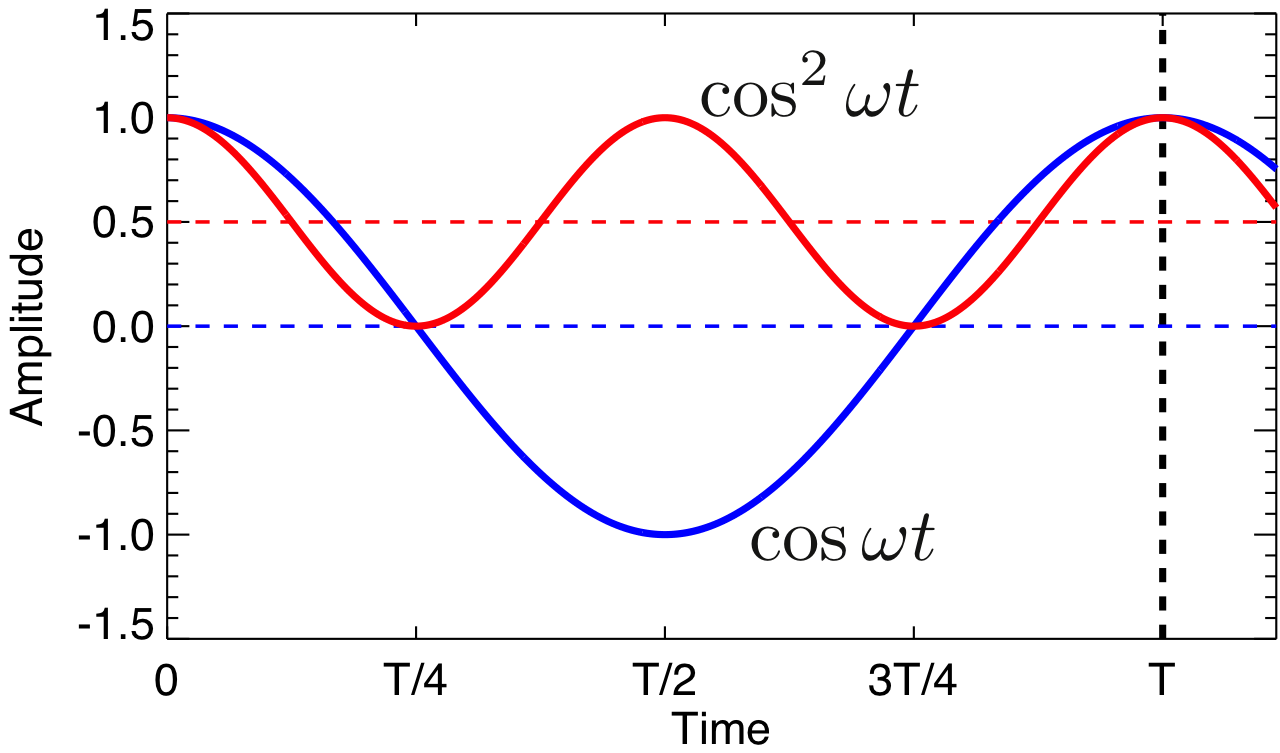
図2. \( \cos \omega t\)と\( \cos^2 \omega t\)の変化
図2で見てわかるように、0から\(T\)までの1周期で平均を取ると
\begin{align} \overline{\cos \omega t} &= 0 \\ \overline{\cos^2 \omega t} &= \frac{1}{2} \end{align}
となる。これを使って式(17)の平均を求めると
\begin{eqnarray} \overline{ \cos k \left( y_0 \pm r_L \cos \omega t \right) } \approx \cos (ky_0)\left( 1 - \frac{1}{4} k^2 r_L^2 \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (18) \end{eqnarray}
である。式(18)を式(13)に代入することで
\begin{eqnarray} \overline{v}_y &=& - \frac{E_0}{B} \cos (ky_0) \left( 1 - \frac{1}{4}k^2 r^2_L \right) \\ &=& - \frac{E(y_0)}{B} \left( 1 - \frac{1}{4}k^2 r^2_L \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (19) \end{eqnarray}
を得る。ExBドリフトでは電場と磁場に垂直な速度は\( \frac{E}{B} \)となる。 今の状況に置き換えると、\(x\)軸正の方向に掛けられた電場と紙面上向きにかけられた磁場によるExBドリフトは\(y\)軸負の向きとなる。 つまり、式(19)の\( - \frac{E(y0)}{B} \)はExBドリフトと同じ大きさ同じ向きを意味しているのである。 よって、式(19)はベクトルを使って書き換えることができて
\begin{eqnarray} v_E &=& \frac{{\bf E}\times {\bf B}}{B^2} \left( 1 - \frac{1}{4}k^2 r^2_L \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (19) \end{eqnarray}
とできるのである。\({\bf E}\)は旋回中心での電場の強さである。 この式(19)は、非一様な電場\(E(y)\)によるプラズマのドリフトの速度である。 よって、旋回中心のドリフト速度であるので、わかりやすいように\( \overline{v}_y \)を\( v_E \)に書き換えた。
この式を少し物理的に考察しようと思う。 式(19)は一様な電場と磁場中のExBドリフトと比べると小さくなる。 この理由は簡単で、電場が場所によって変化する場合、電場が最大な場所に居たとしても円運動の大部分では電場の弱い場所にプラズマは居ることになる。 よって、ドリフト速度は結果的にExBより小さくなるのである。
もっと一般的に考えると、正弦波的に変化する電場によって、プラズマは円運動の1周期で異なる電場を感じる。 この電場を円運動の1周期で平均すると、その円運動の中心である旋回中心での電場\( E(y) \)より小さくなる。 するとやはり、ドリフト速度は旋回中心での電場によるExBドリフトの速度より小さくなるのである。 このようにExBドリフトより小さくなる”修正項”が式(19)の第2項なのである。
また、電場の変化の波長が非常に大きい場合は\( k \)が小さくなる。 すると、第2項は無視できるほど小さくなる。 これは、円運動の1周期でほとんど電場が変わらないことからもわかるだろう。 (電場が直線的に変化する場合も第2項は0になる。)
では、もう少し式(19)を見ていこう。 電場の空間変化は実は以下のようなところから来ている。
\begin{eqnarray} E_0 e^{iky} = E_0 \left( \cos ky + i \sin ky \right)\ \ \ \ \ \ (20) \end{eqnarray}
実際に観測されるのは実部であるので、\(i \sin ky \)は観測されない。 このことから電場を式(1)と置けているのである。 では式(20)を2階微分すると
\begin{eqnarray} \frac{\partial^2}{\partial y^2} E_0 e^{iky} = -k^2 E_0 e^{iky} \ \ \ \ \ \ (21) \end{eqnarray}
となる。もし、電場が三次元的に変化しているとすると、式(21)は
\begin{eqnarray} \nabla^2 E_0 e^{iky} = -k^2 E_0 e^{iky} \ \ \ \ \ \ (22) \end{eqnarray}
である。ここで、\(k\)は3次元に拡張するときに\( k = \sqrt{k_x^2 + k_y^2 + k_z^2} \)としている。 これらのことから、\( \nabla^2 = - k^2 \)であることがわかる。 よって、式(19)を3次元に拡張して、任意の電場に対しては
\begin{eqnarray} v_E &=& \left( 1 + \frac{1}{4} r^2_L \nabla^2 \right) \frac{{\bf E}\times {\bf B}}{B^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (23) \end{eqnarray}
と書けるのである。
式(19)、式(20)からもわかるように、ドリフト速度の式にラーモア半径が入っている。 このラーモア半径が含まれている第2項は有限ラーモア(Larmor)半径効果と呼ばれる。
ラーモア半径は電子とイオンでは大きく異なり、イオンのラーモア半径の方が電子のラーモア半径と比べて大きい。 よって、非一様な電場中でのドリフト速度はイオンの方が小さくなることになる。 これによりイオンと電子で密度差を生じさせ、二次的な電場を生じさせる。
もし、この二次の電場が一次の電場を大きくさせるような機構が働いた時、一次の電場が際限なく大きくなってしまう。 これをドリフト不安定と呼び、別のページで紹介する。 当然のことではあるが、電場の変化が空間的に急激であるような\( k\)が大きい(波長が小さい)場合において、ラーモア半径効果は重要になってくるのである。