ロスコーン
カテゴリー:プラズマ物理学
図1のように\( z \)軸方向に磁場がかけられており、さらに\(z\)軸方向に磁場の強さが変わるような系にプラズマを置いた場合を考える。 この時、弱磁場領域(図1では左側)から強磁場領域(図1では右側)にプラズマが侵入すると、 磁気ミラーによってプラズマは弱磁場領域の方向に反射される。
実はこの磁気ミラーは完全には起こらない。 つまり、ある条件のプラズマは強磁場領域を突き抜けてしまうのである。 では、どのような場合において、強磁場領域をプラズマが抜けてしまうか考える。

図1. 磁場が曲率を持つ場合のプラズマの運動(正電荷の場合)
まず、磁気ミラーがなぜ起こるのかを簡単に説明する。 詳しい説明は磁気ミラーのページを参考にして欲しい。 プラズマに働く磁場に並行な力の成分\( F_{//} \)は
\begin{eqnarray} F_{//} = - \mu \frac{\partial B}{\partial s} = - \mu \nabla_{//} B\ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
となる。ここで、\( s \)は線素で磁力線方向の微小距離である。 \( \mu \)は磁気モーメントで
\begin{eqnarray} \mu = \frac{1}{2} \frac{m v_{\perp}}{B}\ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
と表されるのである。 ここで、\( v_{\perp} \)は磁力線に垂直な方向の速度成分である。 この磁気モーメントは保存される(時間変化しない)ので、強磁場領域にプラズマが侵入すると、磁気モーメントを一定に保つために\( v_{\perp} \)を 大きくしなければならない。しかし、運動エネルギーは一定でなくてはならない。
よってプラズマは、\( v_{\perp} \)を大きくする代わりに磁場に水平な速度成分である\( v_{//} \)を小さくするのである。 このようにして、強磁場領域では\( v_{//} \) がやがて0になってしまい、式(1)で示された力によって反射されるのである。 これが、磁気ミラーの原理である。
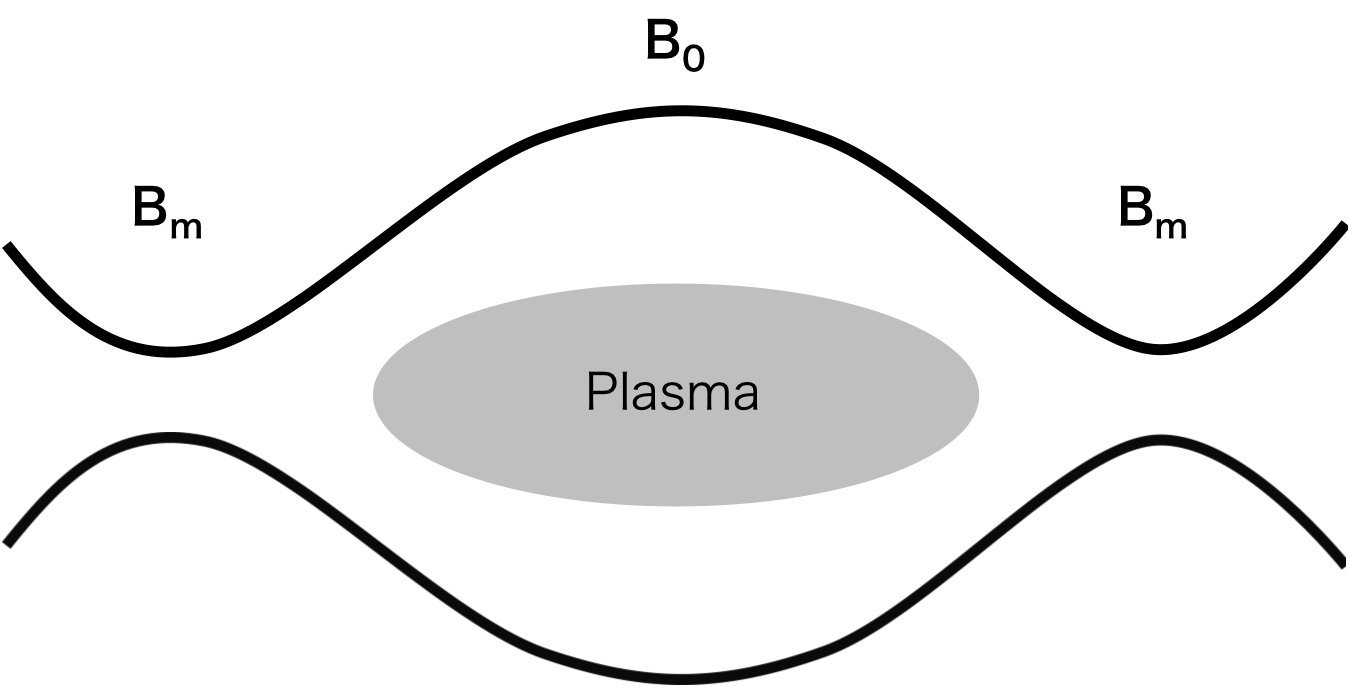
図2. 磁気ミラーによって閉じ込められたプラズマ
ではこの磁気ミラーはどの程度有効なのであろうか?
まず、\( v_{\perp} \)が0のプラズマ、つまり、磁場に完全に沿って運動するプラズマは保存すべき磁気モーメントを持たないので、磁気ミラーは起こらない。 また、このような極端な場合でなくても、\( v_{//} \)が非常に大きい場合は、強磁場領域の磁場が相当強くなければやはりプラズマは通り抜けてしまうだろう。 どうやら、速度成分の比に磁気ミラーが起こるか起こらないかのヒントがあるようである。
図2のように、磁気ミラーによってプラズマを閉じ込める場合を考える。 磁場が最も弱い真ん中の面での磁場を\( B_0 \)とし、そこでのプラズマの磁場に垂直と並行な速度をそれぞれ\( v_{\perp0},\ v_{//0} \)とする。 また、磁場が最も強い面での磁場を\( B_m \)とする。
磁気ミラーが起こる場合は\( B_m \)の面より手前で起こる。 逆に、\( B_m \)の面を超えてしまうと磁気ミラーは起こらないのである。 では、磁気ミラーの反射点で磁場が\( B’ \)、磁場に垂直な速度成分が\( v’_{\perp} \)であるとすると、 磁気モーメントの保存により下の関係式が導ける。
\begin{eqnarray} \frac{1}{2} \frac{m v^2_{\perp 0}}{B_0} = \frac{1}{2} \frac{m v’^2_{\perp}}{B’}\ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
この関係式をもっと整理すると
\begin{eqnarray} \frac{v^2_{\perp 0}}{v’^2_{\perp}} = \frac{B_0}{B’}\ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}
である。
ここで、式(4)をピッチ角という、磁場\( B_0 \)における\( v_{\perp0} \)と\( v_{//0} \)が作る速度ベクトルと磁力線が成す角度の関係とを示したいと思う。 図3にピッチ角についての関係を示したいと思う。 この図は一般的な場合について書いたので、\( v_{\perp0} = v_{\perp}\)、\( v_{//0} = v_{//} \)と置き換えて考えて欲しい。 ここで、プラズマ粒子の速度ベクトル\( v_0 \)の大きさは、
\begin{eqnarray} v_0^2 = v^2_{\perp0} + v^2_{//0}\ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
で表される。図にはこの速度ベクトル\( v_0 \)を示してはいないが、\( v_{\perp0} \)と\( v_{//0} \)とをつなぐ斜めの赤い点線が速度ベクトルの大きさに相当する。 ピッチ角\( \theta \)を\( v_{0} \)と\( v_{\perp 0} \)で表すと
\begin{eqnarray} \sin \theta = \frac{ v_{0} }{ v_{\perp 0} } \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
となる。
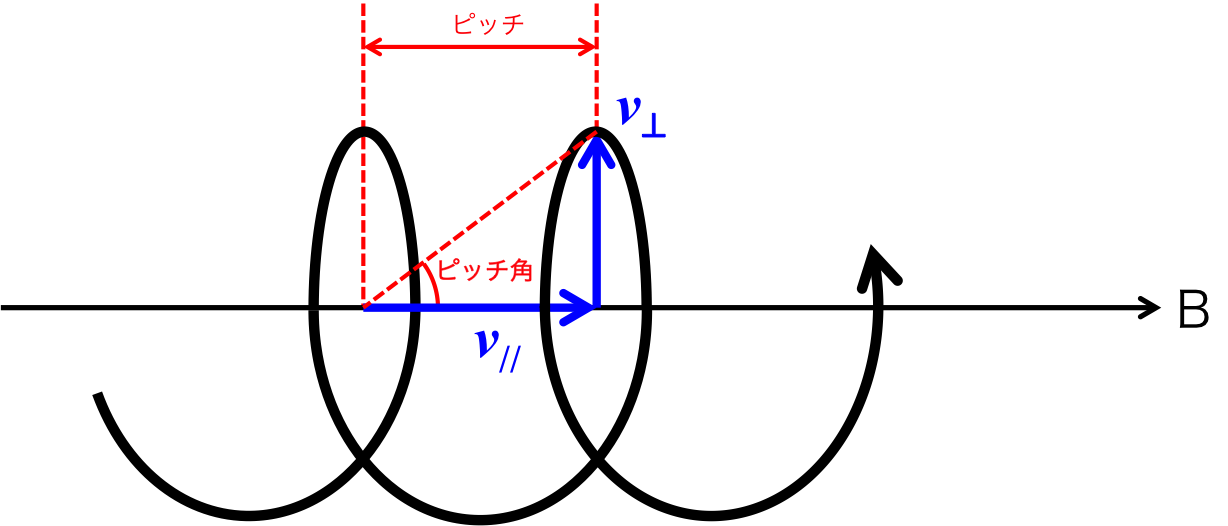
図3. ピッチ角
反射点での速度は\( v’^2_{\perp} \)、\( v_{//0} =0 \)となるので、運動量保存から
\begin{eqnarray} v^2_0 = v^2_{\perp0} + v^2_{//0} = v’^2_{\perp}\ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}
となり、\( v_0^2 = v’^2_{\perp} \)であることが導けるのである。 よって、式(4)、式(6)、式(7)から以下のことが導ける。
\begin{eqnarray} \frac{v^2_{\perp 0}}{v’^2_{\perp}} = \frac{v^2_{\perp 0}}{v^2_{0}} = \frac{B_0}{B’}= \sin^2 \theta\ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray}
ここで、\( \theta \)はピッチ角である。 ここで、もし\( \theta \)が小さければ、\( B’\)が大きくなくてはならない。 もし、その\( B’ \)が最大の磁場である\( B_m \)を超えてしまう時、プラズマを閉じ込めることができなくなるのである。 つまり、式(8)の\( B’\)を\( B_m \)に置き換えて考えて
\begin{eqnarray} \sin^2 \theta_m = \frac{B_0}{B_m} = \frac{1}{R_m} \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray}
を得る。ここで、\( R_m\)はミラー比と呼ばれる磁場の強度比である。 式(8)で得られる\( \theta_m \)より小さいピッチ角を持つプラズマ粒子は反射点を抜けることができるのである。 逆に\( \theta_m \)以上の大きさのピッチ角を持つ粒子は磁気ミラーにより、閉じ込めることができるのである。
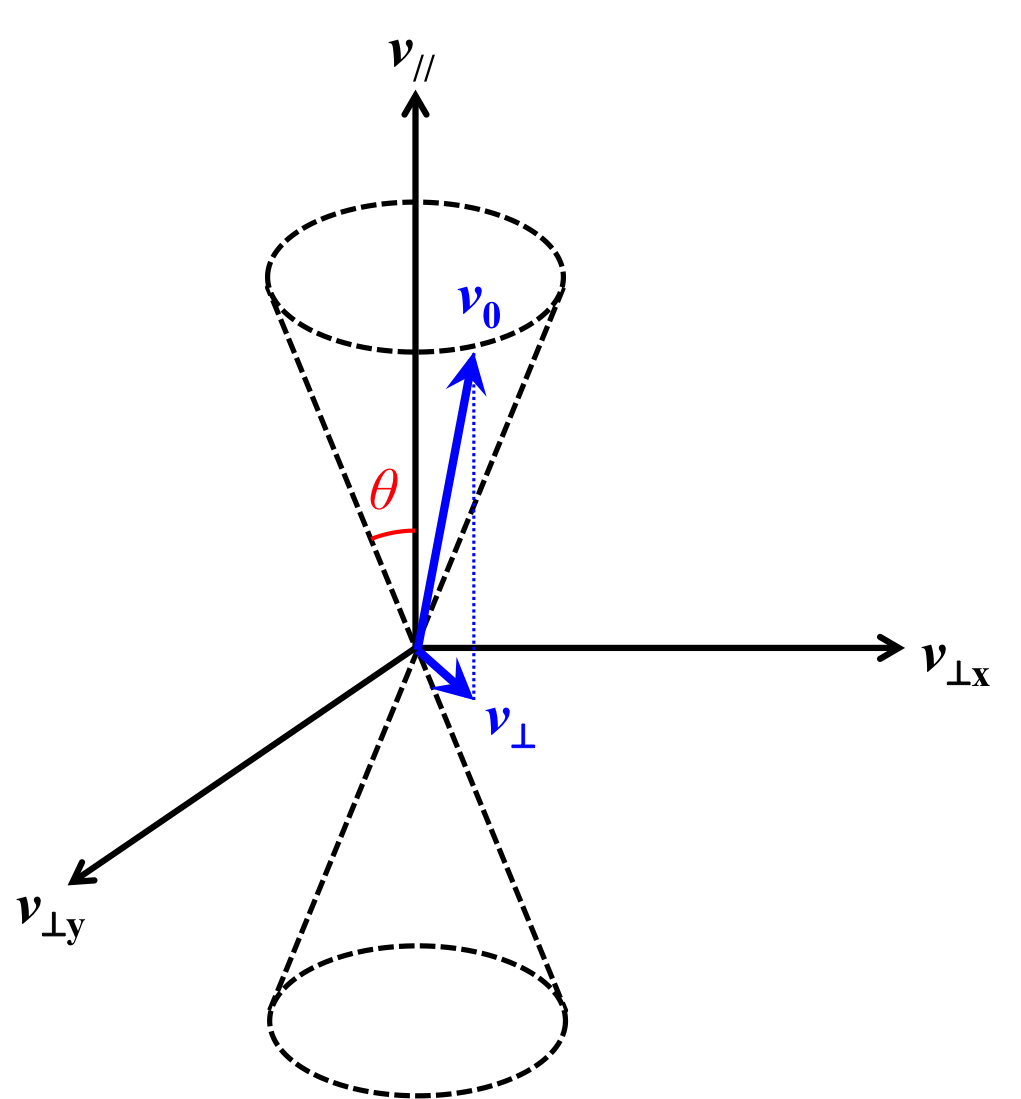
図4. ロスコーン
\( v_{\perp} \)と\( v_{//} \)の速度空間を図4に示す。 \( v_0 \)は\( v_{\perp} \)と\( v_{//} \)のベクトルの足し算で表される。 この時、\( v_{0} \)と\( v_{//} \)の成す角が\( \theta_m \)より小さい時、磁気ミラーによる反射は起こらないのである。
このように、磁気ミラーが起こらない速度分布である、\( v_{0} \)と\( v_{//} \) の成す角が\( \theta_m \)より小さい領域を示すと図4のようなコーン型になる。 このコーンの中に速度\( v_0 \)を持つプラズマは磁気ミラーの反射点で反射されずに失われる(loss:ロス)ので、ロスコーンと呼ばれるのである。