磁場が曲率を持つ場合の運動

図1のように磁場が曲がっている場合を考える。座標系は\( {\bf B} \)の方向に\( \theta \)を取り、磁場が作る円の中心からの距離を\( r \)とする。

この系に、プラズマ粒子を置くとプラズマ粒子は旋回運動をしながら磁場に沿って運動する（図1の赤い点と軌跡がプラズマの運動）。プラズマの磁場の方向に沿った運動に注目してみる。

この時、磁場が曲率を持っている場合、プラズマは遠心力を受ける。（プラズマの旋回運動（回転運動）によって生じる力は1周期で平均することで、消去される。）

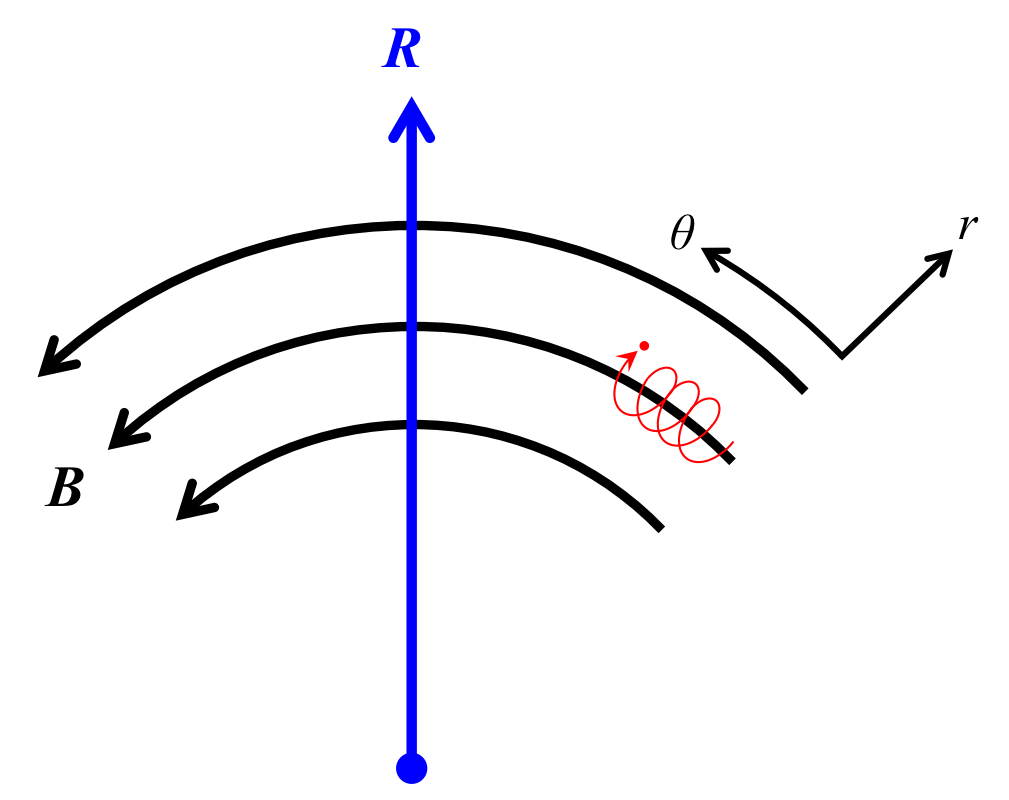
図1 磁場が曲率を持つ場合のプラズマの運動

磁場がかけられた中でプラズマが力を受けるときは、

\begin{eqnarray} {\bf v}_d = \frac{1}{q}\frac{{\bf F}\times {\bf B}}{B^2} \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

のドリフト速度を持つのであった。このように、曲率を持つ磁場中を運動することで遠心力を受けて、プラズマが起こすドリフト運動を曲率ドリフト（Curvature drift）または、湾曲ドリフトと呼ぶ。では、次はどのくらいの速度でドリフトするか求めていく。

曲率ドリフト

まずは、プラズマの旋回中心の運動にかかる遠心力を求める。曲がった磁場はある円の一部と近似することができる。その円の半径を曲率半径と呼ぶ。曲率半径を\( R \)とすると、遠心力は、

\begin{eqnarray} F = m \frac{v_{//}^2}{R}\ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}

と書くことができる。このとき、\( v_{//} \)は磁場に平行なプラズマの速度である。この式(2)は、円運動の遠心力の関係式から導くことができる。式(2)はスカラー量であるので、式(1)に代入するためにはベクトル量に変換しなければならない。よって、式(2)を

\begin{eqnarray} F = m v_{//}^2 \frac{{\bf R}}{R^2} \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}

と書き直す。この式(3)を式(1)に代入することで、曲率ドリフト速度\( {\bf v}_c \)は

\begin{eqnarray} {\bf v}_c = \frac{mv^2_{//}}{qB^2} \frac{{\bf R} \times {\bf B}}{R^2}\ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}

となる。曲率ドリフトも重力ドリフト、磁場勾配ドリフトと同じ様に、電荷によってドリフトの方向が変わるのである。ドリフトの方向は紙面垂直方向で、速度は旋回中心の速度であることに注意する。

曲率ドリフトと磁場勾配ドリフト

磁場が曲率を持つ場合、曲率半径方向に磁場の勾配が必ず生じる。つまり、曲率ドリフトと勾配ドリフトは同時に起こるのである。磁場勾配ドリフトは

\begin{equation} {\bf v}_{\nabla B} = \pm \frac{1}{2} v_{\perp} r_L \frac{{\bf B} \times \nabla B}{B^2}\ \ \ \ \ \ \ \ \ (5) \end{equation}

と表すことができるのである。ここで、\( v_{\perp} \)は磁場に垂直なプラズマの速度（旋回中心の速度ではなく、粒子１つの速度）、\( r_L\)はラーモア半径である。これを式(4)と比較しやすい形にしていく。

図1を円筒座標と考えて、紙面裏から表を\(z\)軸とする。この座標系で、真空中で電流が無い場合は磁場の回転\( \nabla \times {\bf B}\)は0で以下のように書き下せる。

\begin{eqnarray} \nabla \times {\bf B} &=& \left[ \frac{1}{r}\frac{\partial B_z}{\partial\theta} - \frac{\partial B_{\theta}}{\partial z} \right] {\bf e}_r + \left[ \frac{\partial B_r}{\partial z} - \frac{\partial B_z}{\partial r} \right]{\bf e}_{\theta} + \frac{1}{r}\left[ \frac{\partial}{\partial r}\left( rB_{\theta} \right) - \frac{\partial B_r}{\partial \theta} \right]{\bf e}_z = 0\ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}

次に、各項について考えてみる。まず、磁場\( {\bf B} \)は\( \theta \)成分しか持たず、勾配は\( r \)方向しかない。つまり、\( B = B_{\theta} \)であり、\( B(r) \)である。（勾配を取りたいので\(B\)はスカラーで考えないといけない。）よって、式(6)は

\begin{eqnarray} \frac{1}{r}\frac{\partial}{\partial r}\left( rB_{\theta} \right) = 0\ \ \ \ \ \ \ \ \ (7) \end{eqnarray}

とできる。つまり、Aをある定数であるとすると、\(　r B_{\theta} = A \)とできるのである。これは以下のように書き換えることができる。

\begin{eqnarray} B_{\theta} = B = \frac{A}{r}\ \ \ \ \ \ \ (8) \end{eqnarray}

である。式(8)の勾配を求めると、

\begin{eqnarray} \nabla B = - \frac{A}{r^2}\ \ \ \ \ \ \ (9) \end{eqnarray}

と求めることができる。式(8)と式(9)より、

\begin{eqnarray} \frac{\nabla B}{B} = - \frac{1}{r}{\bf e}_r = - \frac{{\bf R}}{R^2}\ \ \ \ \ \ \ (10) \end{eqnarray}

とできる。この式(10)を式(5)に代入し、ラーモア半径\( r_L \)が

\begin{eqnarray} r_L = \frac{mv_{\perp}}{|q|B} \end{eqnarray}

で表されることを使って、

< \begin{eqnarray} v_{\nabla B} = \frac{1}{2} \frac{m}{q} v^2_{\perp} \frac{{\bf R} \times {\bf B}}{R^2B^2}\ \ \ \ \ \ (11) \end{eqnarray}

と導くことができる。（ラーモア半径を代入する時に電荷によって、+と-を掛けなければならないことに注意する）つまり、曲率を持つ磁場に置かれたプラズマは、曲率ドリフトと磁場勾配ドリフトを起こす。その速度は足し合わせることで、

\begin{eqnarray} {\bf v}_c + {\bf v}_{\nabla B} = \frac{m}{q} \frac{{\bf R}\times {\bf B}}{R^2B^2} \left( v_{//} + \frac{1}{2}v_{\perp} \right)\ \ \ \ \ \ \ \ \ \ (12) \end{eqnarray}

と表すことができる。