一様な磁場と重力場中の運動

重力場と磁場中のプラズマの運動を考える。

地球の高層大気は大気の一部が太陽の極端紫外線によって電離されており、地球の磁場と重力によりこのような状況になっている。この場合の運動方程式は

\begin{equation} m \frac{d {\bf v}}{dt} = m {\bf g} + q{\bf v} \times {\bf B}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{equation}

となる。プラズマ粒子の運動を追うためにはこの方程式を\( x,/ y,/ z \)方向に分解して考えなくてはならないがこれは、一様な磁場・電場中の運動の運動方程式の\( q {\bf E} \)を\( m {\bf g} \)に変えただけなので、ここでは、旋回中心（プラズマの回転運動の中心）の運動に注目する。

式(1)の左辺の加速度の項はプラズマに回転運動を与えているだけなので、旋回中心の運動を見るときは0とすることができる。よって、

\begin{equation} m {\bf g} + q{\bf v} \times {\bf B} = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{equation}

である。この式に右から磁場ベクトル\( {\bf B} \)の外積を掛ける。

\begin{equation} m {\bf g} \times {\bf B} + q{\bf v} \times {\bf B}\times {\bf B} = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{equation}

左辺第二項はベクトル三重積で

\begin{equation} \frac{m}{q} {\bf g} \times {\bf B} = ({\bf B} \cdot {\bf B}){\bf v} - ({\bf v} \cdot {\bf B}){\bf B}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{equation}

と書き直すことができる。磁場垂直な速度成分\( {\bf v}_{\perp} \)を考えると、速度と磁場の内積である右辺第２項は消え、第１項は\( B^2{\bf v} \)となる。整理すると、

\begin{equation} {\bf v}_{\perp} = \frac{m}{q} \frac{{\bf g} \times {\bf B}}{B^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{equation}

を導くことができる。この式に着目すると、プラズマ粒子の電荷によってドリフト速度が異なることがわかる。これを図解すると、図1のようになる。

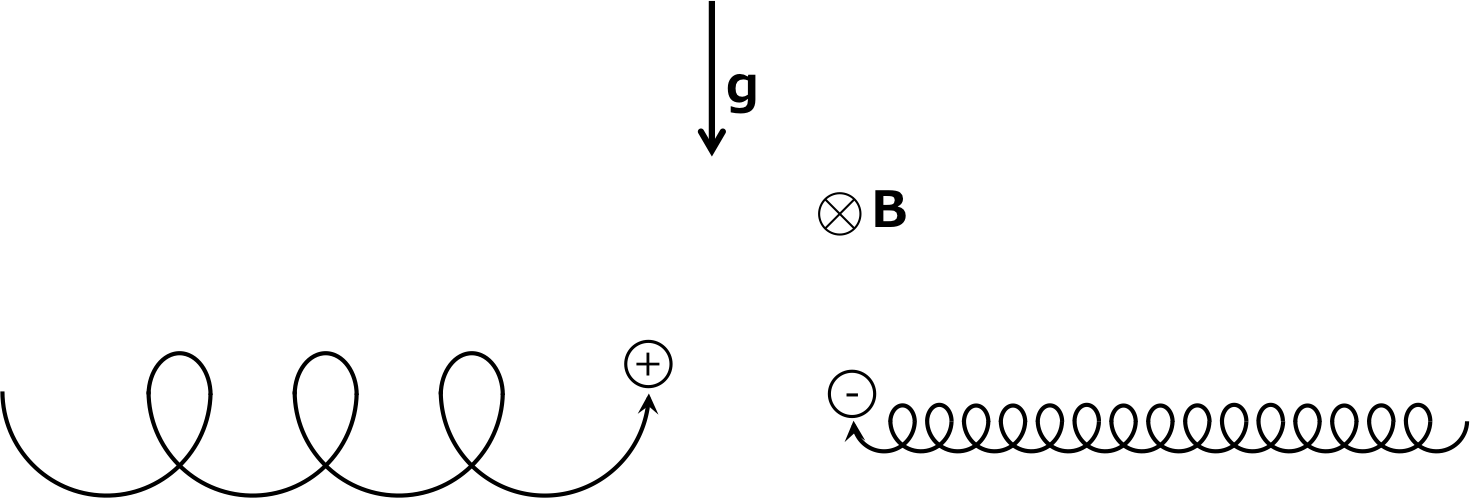
図1 磁場と重力場中の電子とイオン

このように磁場と重力場中のプラズマはその電荷の違いによってドリフト方向が異なる。これはこの中に電流を生じさせることを意味する。

電流はそれぞれの電荷を持つプラズマ粒子の速度差に密度を掛け合わせて表され、電子の進む方向と逆方向に流れる。つまり、磁場と重力場中におかれたプラズマは

\begin{equation} {\bf j} = n ({\bf v}_{+} - {\bf v}_{-}) = n(M+m)\frac{{\bf g} \times {\bf B}}{B^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{equation}

の電流を流すことがわかる。ここで、\( M \)はイオンの質量、\( m \)は電子の質量、\( n \)はプラズマの密度である。プラズマの密度はイオンと電子で等しいとしている。