一様な磁場と電場中の運動

磁場と電場中に存在するプラズマはどのような運動をするのだろう？

この問題を解くためにはまずプラズマ粒子の運動と、旋回中心（回転運動の中心）の運動に分けて考えることが重要である。はじめに、図1のようなz軸方向に磁場が、x軸方向に電場がかかっている系を考える。

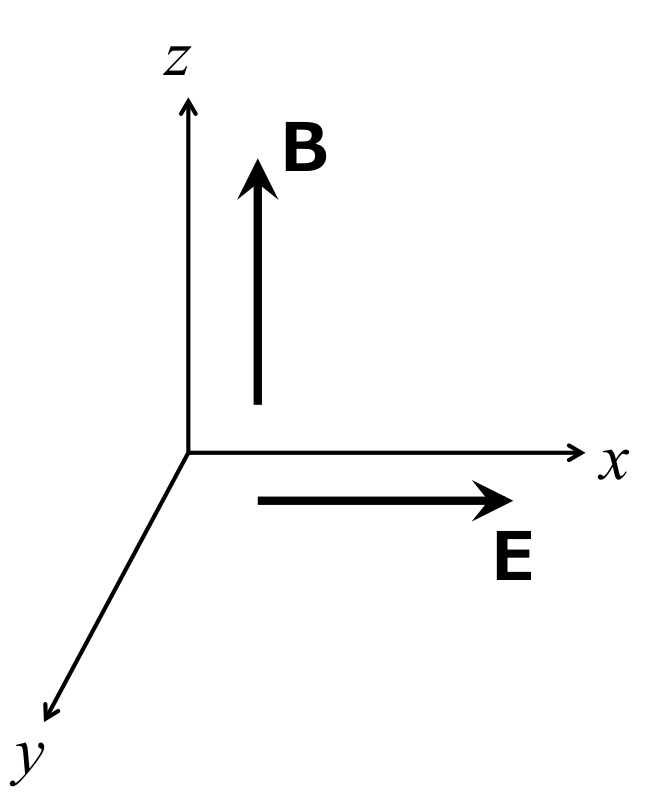
図1 z軸方向に磁場がx軸方向に磁場がかけられた系

この系でのプラズマの運動方程式は

\begin{equation} m \frac{d {\bf v}}{dt} = q \left( {\bf E} + {\bf v} \times {\bf B} \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{equation}

である。右辺の第1項は電場による力、第2項は磁場によるローレンツ力が表されている。

それでは、プラズマ粒子１つの運動と、旋回中心の運動に分けて考えていく。

粒子の運動

式(1)の運動方程式をベクトルの成分、\( x,\ y,\ z\)ごとに分解すると以下のようになる。

\begin{eqnarray} \frac{d}{dt} v_{x} &=& \dot{v_{x}} = \frac{q}{m}E_{x} + \frac{v_y qB}{m} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \\ \frac{d}{dt} v_{y} &=& \dot{v_{y}} =- \frac{v_x qB}{m} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \\ \frac{d}{dt} v_{z} &=& \dot{v_{z}} = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}

ここでサイクロトロン周波数（ジャイロ周波数、旋回周波数）

\begin{equation} \omega = \frac{|q|B}{m}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{equation}

を使って、式(2)、(3)、(4)を書き直すと

\begin{eqnarray} \dot{v_{x}} &=& \frac{q}{m}E_{x} \pm \omega v_y \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \\ \dot{v_{y}} &=& \mp \omega v_x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \\ \end{eqnarray}

であることがわかる。ここで、\( \omega \)の前の符号は電子とイオンによる（上がイオン、下が電子）。式(6)、(7)をもう一度微分すると

\begin{eqnarray} \ddot{v_{x}} &=& \pm \omega \dot{v_y} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \\ \ddot{v_{y}} &=& \mp \omega \dot{v_x} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \\ \end{eqnarray}

となる。式(6)から(9)までの式を連立方程式として解くと、

\begin{eqnarray} \ddot{v_{x}} &=& - \omega^2 v_x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (10) \\ \ddot{v_{y}} &=& \mp \left( \frac{q}{m}E_x \pm \omega v_y \right) = - \omega^2 \left( v_y + \frac{E_x}{B} \right) \ \ \ \ \ \ \ \ \ \ \ \ (11) \\ \end{eqnarray}
を得る。式(10)の微分方程式を解くと、

\begin{equation} v_x = v_{\perp} e^{i \omega t} \ \ \ \ \ \ \ \ \ \ (12) \end{equation}

を得る。\( v_{\perp} \)は磁場に垂直な速度である。これを式(6)に代入することで、

\begin{equation} v_y = \pm i v_{\perp} e^{i \omega t} - \frac{E_x}{B}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (13) \end{equation}

を得る。\( e^{i\omega t} \)は

\begin{equation} e^{i\omega t} = \cos( \omega t) + i \sin ( \omega t )\ \ \ \ \ \ \ \ \ \ (14) \end{equation}

と展開できる。実際に観測されるのは実数部分である。 \( v_x \)と\( v_{y} \)に式(13)を代入し、実数部分を見ることで、プラズマ粒子は回転することがわかる。しかし、y方向には\( \frac{E_x}{B} \)の速度でドリフトしていくことがわかる。回転しながらのドリフトを図解すると、図2のように表される。

このことからわかるように、イオンと電子は同じ方向にドリフトするが、回転の向きは反対になるのである。このドリフトを\( E \)クロス\( B \)（いーくろすびー）ドリフトと呼ぶ。

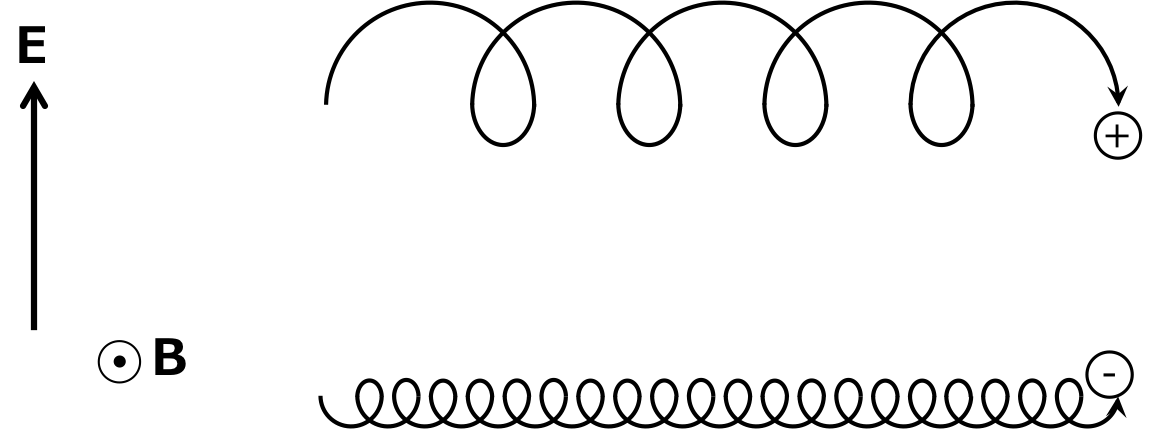
図2 磁場と電場中の電子とイオン

旋回中心の運動

磁場と電場中のプラズマの運動方程式をもう一度示す。

\begin{equation} m \frac{d {\bf v}}{dt} = q \left( {\bf E} + {\bf v} \times {\bf B} \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{equation}

ここで、右辺は速度の時間変化の項で加速度を表す。この加速度は回転を作り出すためのものである（回転には中心に向かう加速度が必要である）。つまり、旋回中心の運動を求める時は式(1)の右辺を0とできるのである。

\begin{equation} {\bf E} + {\bf v} \times {\bf B} = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (15) \end{equation}

として、右から\( {\bf B} \)との外積を取ると

\begin{equation} {\bf E} \times {\bf B} + {\bf v} \times {\bf B} \times {\bf B}= 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (16) \end{equation}

となる。左辺第二項はベクトル三重積であるので簡単に解ける。解いてみると、

\begin{equation} {\bf E} \times {\bf B} + ({\bf v} \cdot {\bf B}){\bf B} + B^2 {\bf v}= 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (17) \end{equation}

となる。磁場に垂直な方向の成分だけ取り出すと、磁場と速度の内積\( {\bf v} \cdot {\bf B} \)は0なる。つまり、磁場に垂直な旋回中心の速度ベクトル\( {\bf v}_{\perp} \)は

\begin{equation} {\bf v}_{\perp} = \frac{{\bf E} \times {\bf B}}{B^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (18) \end{equation}

となる。上で示したように、これは、磁場と電場中のプラズマの旋回中心の速度が電場と磁場の外積で表される、\( E \)クロス\(B \)ドリフトである。ここで注目したいのが、やはり、\( E \)クロス\(B\)ドリフトはプラズマの電荷によらない。つまり、電子とイオンではドリフトの方向は同じになるのである。