一様な磁場中の運動
カテゴリー:プラズマ物理学
一様な磁場中でのプラズマの運動を考える。 一様な磁場中ではプラズマはローレンツ力を受ける。 運動方程式を立ててみると、
\begin{equation} m \frac{d}{dt} v = q {\bf v} \times {\bf B}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{equation}
である。 簡単のために、磁場は図1のようにz方向にしかかかっていないと仮定する。 つまり、\( {\bf B} = (0,\ 0,\ B_z) \)である。
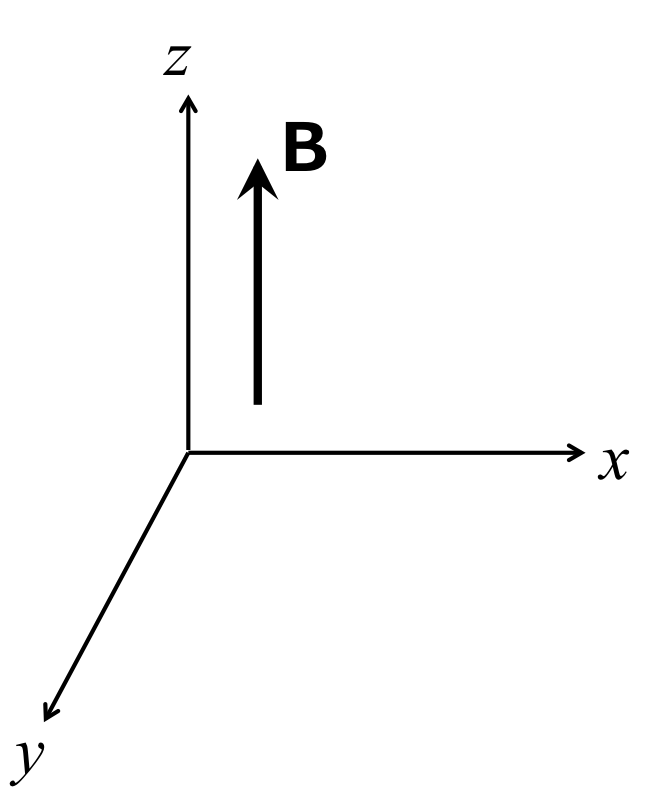
図1 磁場のかかる方向
この条件で運動方程式(1)の右辺の外積を計算し、x, y, z方向の速度成分に分解すると以下のようになる。
\begin{eqnarray} \frac{d}{dt} v_x &=& \dot{v_x} = \frac{q}{m} \left( v_y B_z \right) \\ \frac{d}{dt} v_y &=& \dot{v_y} = \frac{q}{m} \left( - v_x B_z \right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \\ \frac{d}{dt} v_z &=& \dot{v_z} = 0 \end{eqnarray}
なり、z方向の速度は時間変化しないことがわかる。これはz方向に対して静止しているか、等速直線運動をしていることを示している。 式(2)をもう一度時間で微分すると、
\begin{eqnarray} \frac{d^2}{dt^2} v_x &=& \ddot{v_x} = \frac{q}{m} \left( \dot{ v_y } B_z \right) \\ \frac{d^2}{dt^2} v_y &=& \ddot{v_y} = \frac{q}{m} \left( - \dot{ v_x } B_z \right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \\ \frac{d^2}{dt^2} v_z &=& \ddot{v_z} = 0 \end{eqnarray}
を得る。式(2)と式(3)から
\begin{eqnarray} \frac{d^2}{dt^2} v_x &=& \ddot{v_x} = - \left( \frac{q B_z}{m}\right)^2 v_x \\ \frac{d^2}{dt^2} v_y &=& \ddot{v_y} = - \left( \frac{q B_z}{m}\right)^2 v_y \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \\ \end{eqnarray}
を得る。これは、簡単な2階同次微分方程式である。ここで、
\begin{equation} \omega = \frac{ |q| B_z}{m} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{equation}
として、式(4)を解くと、
\begin{eqnarray} v_x &=& v_{\perp} \mathrm{e}^\left( { i\omega t} + \delta_{x} \right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \\ v_y &=& v_{\perp} \mathrm{e}^\left( { i\omega t} + \delta_{y} \right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
となる。ここで、\( v_{\perp} \)は磁場に垂直(\(xy\)平面)な粒子の速度、\( \delta_x,\ \delta_y \)は\(v_{x},\ v_{y}\)の初期位相である。 ここで、\( \delta_x = 0 \)と置いて計算を進めてみる。
\begin{eqnarray} v_x &=& v_{\perp} \mathrm{e}^{i\omega t} = v_{\perp} \cos \omega t + i v_{\perp} \sin \omega t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}
である。式(7)を微分すると、
\begin{eqnarray} \frac{d}{dt}v_x &=& \dot{v_x} = \frac{v_{\perp}}{i \omega} \mathrm{e}^{i\omega t} = \frac{v_{\perp}}{i \omega} \cos \omega t + \frac{v_{\perp}}{\omega} \sin \omega t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray}
を得る。式(2)と式(8)から\( v_y \)に関する以下の式を得る。
\begin{eqnarray} v_y &=& \frac{1}{\omega} \dot{v_x} = - v_{\perp} i \cos \omega t + v_{\perp} \sin \omega t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray}
実際に運動として観測されるのは実部の部分であるので、粒子の速度は以下のように示される。
\begin{eqnarray} v_x &=& v_{\perp} \cos \omega t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (10) \\ v_y &=& \pm v_{\perp} \sin \omega t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (11) \end{eqnarray}
速度のy成分の\( \pm \)は電荷\( q \)が正か負かで決まる。 電子の場合は \(q=-q\) なのでマイナスが付く。
まずイオン(\(q\)が正)の場合を計算してみる。 速度を積分することで、粒子の位置の時間変化を得る。
\begin{eqnarray} \int v_x\ dt &=& x = \frac{v_{\perp}}{\omega} \sin \omega t + x_0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (12) \\ \int v_y\ dt &=& y = -\frac{v_{\perp}}{\omega} \cos \omega t + y_0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (13) \end{eqnarray}
ここで、\(x_0,\ y_0\)は定数であり後に出てくる回転運動の中心を意味する。 位置の変化の式から磁場中のプラズマは磁場に垂直な面で回転運動をすることがわかる。
式(12)、(13)は正の電荷を持ったイオンに対しての式である。 電子に対しては\( q = -q \)として解くことで、
\begin{eqnarray} \int v_x\ dt &=& x = \frac{v_{\perp}}{\omega} \sin \omega t + x_0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (12) \\ \int v_y\ dt &=& y = \frac{v_{\perp}}{\omega} \cos \omega t + y_0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (13) \end{eqnarray}
となり、イオンとは逆方向に回転する。その半径はラーモア半径\( r_L \)と呼ばれ、
\begin{eqnarray} r_L = \frac{v_{\perp}}{\omega} = \frac{mv_{\perp}}{ |q| B_z} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (14) \end{eqnarray}
と表される。プラズマの質量差から電子の方がラーモア半径は小さくなる。 また、磁場が大きければ大きいほど、ラーモア半径は小さくなる。
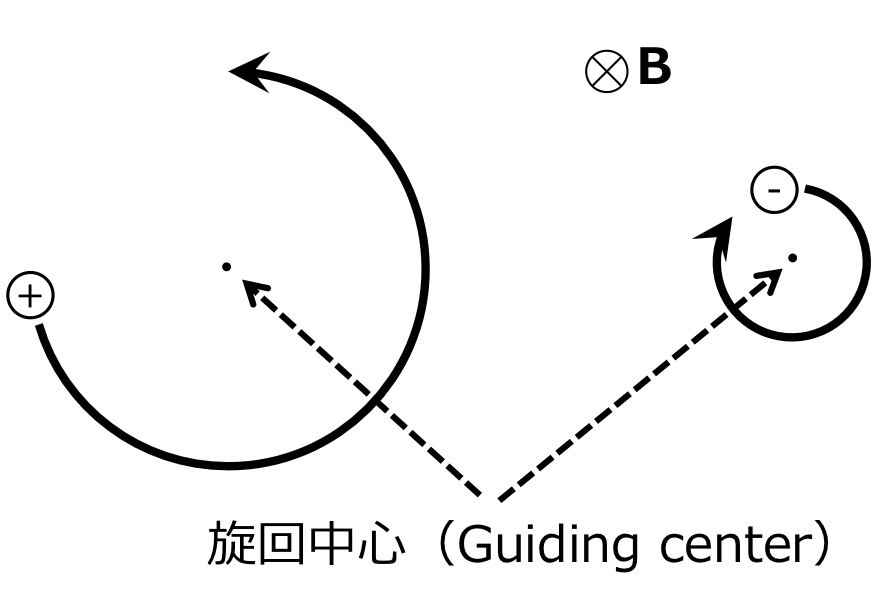
図2 電子(右)とイオン(左)の磁場中での運動。それぞれ、ラーモア半径と回転方向が異なる。
回転の中心は旋回中心と呼ばれ、英語ではGuiding Centerと呼ばれる。 プラズマ物理ではこの旋回中心の運動を取り扱う場合と、粒子の運動を取り扱う場合があるので、 常に注意が必要である。