ラーモア半径
カテゴリー:プラズマ物理学
磁場の中に電子(負電荷)とイオン(正電荷)を起き、初速度を与えると回転運動を始める。 これは、ローレンツ力を受けて円運動の中心向きの加速度が生じるためである。 ローレンツ力は電荷の正負によって方向が異なるので負電荷と正電荷では回転の方向が反対となるのである(図1)。 この回転運動の半径\( r_L \)は、
\begin{eqnarray} r_L = \frac{v_{\perp}}{\omega} = \frac{mv_{\perp}}{ |q| B_z} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
で与えられる。この半径\( r_L \)のことをラーモア半径、またはラーマー半径と呼ばれる。
式からも分かるように、磁場が強ければラーモア半径は小さくなる。 また、同じ磁場中を運動する場合、質量の大きい粒子(通常は正電荷)の方がラーモア半径は大きい。
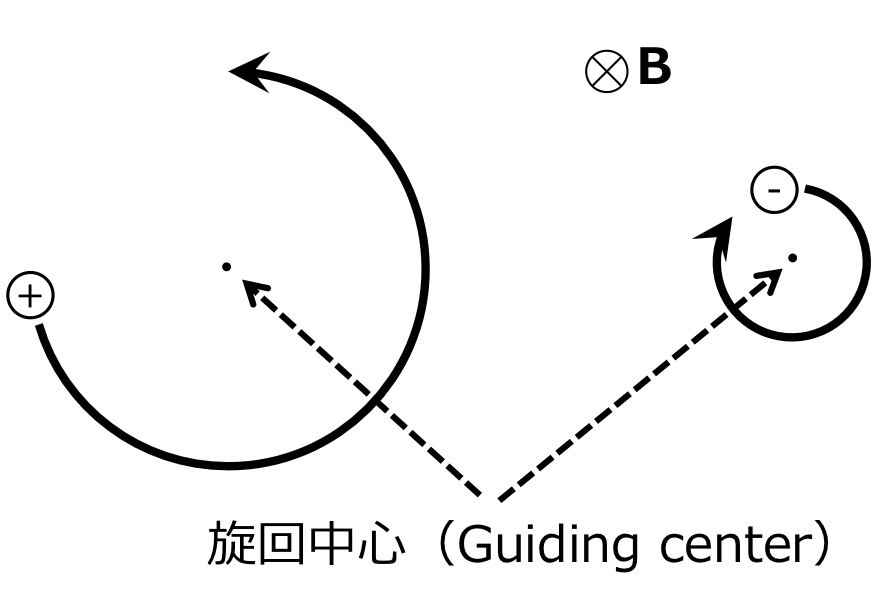
図1 電子(右)とイオン(左)の磁場中での運動。それぞれ、ラーモア半径と回転方向が異なる。
ラーモア半径は、プラズマの運動方程式から導出される。 導出の詳しい説明は、プラズマの一様な磁場中の運動のページで紹介しているので、そのページを参考にしてほしい。
スポンサーリンク