デバイ長
カテゴリー:プラズマ物理学
考えているスケール(現象のスケール)が、デバイ長より短い長さであれば、デバイ遮蔽は有効ではなく、デバイ長より長ければデバイ遮蔽が十分有効であると考える。
これは、通常プラズマは準中性であるので、イオンと電子の電荷分布は等しいが、デバイ長以内では電子とイオンが個々に運動しており、別々の電荷分布を持つことを意味している。
ここでは、デバイ長の考え方と求め方(導出方法)を紹介していく。
プラズマ中に電極が入るとデバイ遮蔽によってプラズマが移動し電極によって作り出される電場を打ち消してしまう。 このデバイ遮蔽は実は完璧に電場を打ち消すわけではない。
プラズマ中に電極が入れられ、電場がかかると、すぐにプラズマが移動を始める。 負極には正イオンが、正極には電子が集まってくる。この状態はプラズマの密度が一様でないことを示す。
一方で、プラズマはマクスウェル・ボルツマン分布に従った熱運動をしている(速度分布を持っている)。 熱運動は密度の非一様を解消する方向に働くのである。
つまり、電極が挿入されるとプラズマ遮蔽により密度が非一様になるが、 熱運動によってそれを解消しようとする相反する力が働くのである。 これにより、プラズマ中にかけられた電場は「そのほとんど」が遮蔽するのみであって、 「ほんの一部」は残されてしまう。
どこに電場が残るのかを想像すると、それはもちろん電極周りのごく薄い領域である。 もっと簡単に言うと、電極から離れれば離れるほど、デバイ遮蔽は完璧になり、近づけば近づくほど電場が現れ始めるのである。 では、どの程度離れればプラズマ遮蔽されたと言えるのかを考える。
デバイ遮蔽が起こると、電子とイオンの密度が非一様になる。 密度に非一様が生じると、熱運動によってプラズマはその密度の非一様を解消しようとする。
電子はイオンに比べて非常に軽いので、早く動くことができて、熱運動によって電子とイオンに速度差が生まれる。 これは平衡状態のプラズマ密度を平均(または背景)であると考えると、そこから電子の密度にムラが生じている状態である。 どういうことかと言うと、何もない空間に電子密度\( \rho \)の領域が置かれたことと同じになる。 密度\( \rho \)が生じると、ガウスの法則により、
\begin{eqnarray} \nabla \cdot {\bf E} = \frac{\rho}{\epsilon_0}\ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
が得られる。この時、
\begin{eqnarray} {\bf E} = - \nabla \phi \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
の関係式を導入すると、式(1)は
\begin{eqnarray} \nabla \cdot {\bf E} &=& \nabla \cdot \left( - \nabla \phi \right) \\ &=& - \nabla^2 \phi = \frac{\rho}{\epsilon_0}\ \ \ \ \ \ \ \ \ (3.1) \end{eqnarray}
の関係式が導かれる。式(1)をポアソン方程式と呼び、1次元の場合のポアソン方程式は図1のようになる。
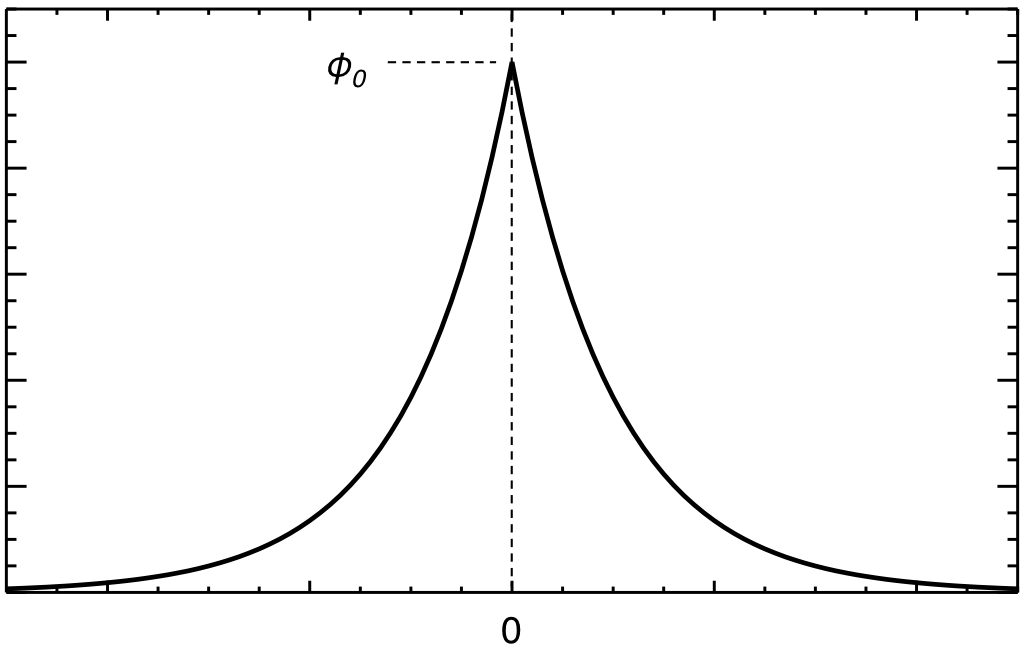
図1. 1次元のポアソン分布
式(1)のポアソン方程式を綺麗にすると、
\begin{equation} \nabla^2 \phi = - \frac{\rho}{\epsilon_0}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3.2) \end{equation}
となる。\( \phi \)はポテンシャルで、どの範囲までポテンシャルが影響を与えるかを計算していく。
このポテンシャルが影響を及ぼす範囲(ポテンシャルがある程度の大きさを持つ範囲)をデバイ長と呼んでいるのである。 ポアソン方程式の\( \rho \)は電荷の分布、\( \epsilon_0 \)は真空透磁率である。 これを1次元で解くと
\begin{equation} \frac{\partial^2}{\partial x^2} \phi = - \frac{e(n_i - n_e)}{\epsilon_0}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{equation}
となる。ここで、無限遠でのイオンと電子の密度が\( n_{\infty} \)だとすると、式(4)の\( n_i = n_{\infty} \)である。 (\( n_e \)は無限遠では\( n_{\infty} \)となるが、x=0付近では\( n_i \ne n_e \)であり、\( n_e \ne n_{\infty} \)である。) つまり、
\begin{equation} \frac{\partial^2}{\partial x^2} \phi = - \frac{e(n_{\infty} - n_e)}{\epsilon_0}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{equation}
である。
次に、ポテンシャル(電位)が存在する場合での電子の分布関数から電子の密度を求めてみる。 電子の分布関数は
\begin{equation} f(u) = n_e \left( \frac{m}{2\pi k_B T_e} \right)^{1/2} \exp \left\{ - (\frac{1}{2}mu^2 - e\phi)/ k_B T_e \right\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{equation}
となる。この分布関数の詳しい導出方法はここでは記さないが、この式はポテンシャルが低いところには少数の電子しかいないということを意味する。 イオンの場合はポテンシャルの符号が逆になるので、ポテンシャルが高いところには少数の粒子しかいないことになる。 式(6)を0から無限大で積分すると、
\begin{eqnarray} n_e = \int_0^{\infty} f(u) du &=& n_e \sqrt{ \frac{m}{2\pi k_B T_e} } \left\{ \sqrt{\frac{2 \pi k_B T_e}{m}} \exp\left\{ \frac{e \phi}{k_B T_e} \right\} \right\} \\ &=& n_e \exp\left\{ \frac{e \phi}{k_B T_e} \right\} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}
この積分にはガウス積分を用いた。ここで、無限遠では\( n_i = n_e = n_{\infty} \)であり、\( \phi = 0 \)であることを考えると、式(7)は以下のように書き換えられる。
\begin{equation} n_e = n_{\infty} \exp\left\{ \frac{e \phi}{k_B T_e} \right\} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{equation}
式(5)と式(8)から、
\begin{equation} \frac{\partial^2}{\partial x^2} \phi = \frac{e}{\epsilon_0} \left\{ \exp\left\{ \frac{e\phi}{k_B T_e} \right\} - 1\right\} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{equation}
式(9)に関して、細かい計算は省くが\( e\phi / k_B T_e \ll 1 \)である場合、指数関数をテイラー展開することができて、
\begin{equation} \frac{\partial^2}{\partial x^2} \phi = \frac{e n_{\infty}}{\epsilon_0} \left\{ \exp\left\{ \frac{e\phi}{k_B T_e} \right\} - 1\right\} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (10) \end{equation}
である。
\begin{equation} \frac{\partial^2}{\partial x^2} \phi = \frac{e n_{\infty}}{\epsilon_0} \left\{ \frac{e\phi}{k_B T_e} + \frac{1}{2} \left( \frac{e\phi}{k_B T_e} \right)^{2} + \cdots \right\} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (11) \end{equation}
となる。ここで、2次の項以下を無視すると、
\begin{equation} \frac{\partial^2}{\partial x^2} \phi = \frac{e^2 n_{\infty}}{\epsilon_0 k_B T_e}\phi \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (12) \end{equation}
を得る。ここで、
\begin{equation} \lambda_D = \left( \frac{\epsilon_0 k_B T_e}{e^2 n} \right)^{1/2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (13) \end{equation}
とすると、式(12)は、
\begin{equation} \phi = C_1 \exp {(|x| / \lambda_D)} + C_2 \exp {(-|x| / \lambda_D)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (14) \end{equation}
である。ここで、\( C_1 \)、\( C_2 \)は定数である。次に、\( x \rightarrow \infty \)で、\( \phi =0 \)であることと、\( x=0 \)で\( \phi = \phi_0 \)である条件を使って、
\begin{equation} \phi = \phi_0 \exp {(-|x| / \lambda_D)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (15) \end{equation}
と\( \phi \)を求めることができるのである。\( \lambda_D \)はデバイ長と呼ばれ、この距離以内であれば、プラズマによるデバイ遮蔽は弱いが、 デバイ長を超えるとほぼ完全にプラズマ遮蔽される。言い換えると、デバイ長以内なら電子とイオンに分かれて電場を生み出すことができるが、 デバイ長以上だとその影響は指数関数的に落ちていく。
すこしデバイ長について考察する。 デバイ長は電子温度が高ければ高いほど大きくなり、電子温度が0に近づくと、デバイ長つまり、電極まわりのデバイ遮蔽されていない領域は無限に小さくなっていく。 これは、プラズマ密度が大きくなっても同じことが言える。