温度の概念(温度とエネルギーの関係)
カテゴリー:プラズマ物理学
高校物理では温度が高い物質の分子または原子は高速度で運動していることを直感的に教えられる。 これは間違っていないが、実際はもう少し補足が必要である。
例えば、300 Kと言うと、全部の粒子が同じ速度で運動しているのではなく、中にはものすごい低速で運動しているものや 高速で運動しているものもある。つまり、粒子は温度によって異なる速度分布を持っているのである。
粒子が取るもっとも確からしい速度分布はマクスウェル(Maxwell)分布として知られている。 簡単のためにまずは以下のような1次元のマクスウェル分布を考える。
\begin{equation} f(u) = \left( \frac{m}{2 \pi k_B T} \right)^{1/2} \exp \left( -\frac{1}{2} \frac{mu^2}{k_B T} \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{equation}
窒素分子の温度の違いによるマクスウェル分布の違いを図1に示す。
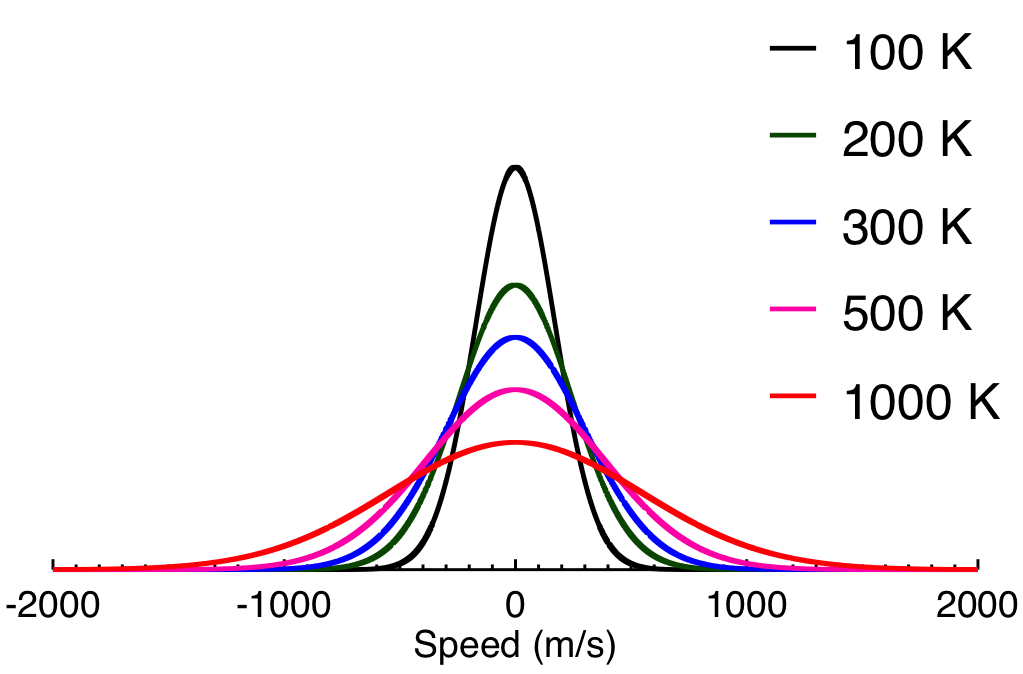
図1 窒素分子のマクスウェル分布
温度が高いほど、分布が広がっており、高速の粒子が多く存在することがわかる。 また、温度が低ければ低いほど粒子が持つ速度の幅が狭いのである。(これは1次元の速度分布であることに注意する。)
この1次元のマクスウェル分布から与えられるのは、分布内に存在する 粒子の中の一つがどの速度で運動しているかという確率分布と言うことができる。 密度\( n \)とマクスウェル分布との関係は以下のように表すことができる。
\begin{equation} n = \int_{-\infty}^{\infty} n f(u)\ du\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{equation}
また同様にして、運動エネルギーの合計は、
\begin{equation} E_{total} = \int_{-\infty}^{\infty} \frac{1}{2}m u^2 n\ f(u)\ du\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{equation}
と表すことができる。これらからこの分布の平均運動エネルギー\( E_{ave} \)を表すと以下のようになる。
\begin{equation} E_{ave} = \frac{E_{total}}{n} = \frac{\int_{-\infty}^{\infty} \frac{1}{2}m u^2\ n f(u)\ du}{\int_{-\infty}^{\infty} n f(u)\ du}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{equation}
ここで、
\begin{eqnarray} v_{th} &=& \left( \frac{2k_B T}{m} \right) ^ {1/2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \\ y &=& \frac{u}{v_{th}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \\ du &=& v_{th}\ dy \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}
とすると、式(1)は
\begin{equation} f(u) = A \exp \left( -u^2 / v_{th}^2 \right) = A \exp \left( -y^2 \right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{equation}
と書き直すことができる。ここで、\( A = \left( m / 2 \pi k_B T \right)^{1/2} \)である。この関係性を用いて、式(4)は
\begin{equation} E_{ave} = \frac{\frac{1}{2}m n A\ v^3_{th} \int_{-\infty}^{\infty} \left\{ \exp (-y^2) \right\}y^2\ dy } {nA\ v_{th} \int_{-\infty}^{\infty} \exp (-y^2)\ dy} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{equation}
となる。分子は以下の様に部分積分をすることができる。
\begin{eqnarray} \int_{-\infty}^{\infty} \left\{ y \exp(-y^2) \right\} y\ dy &=& \left[ \left\{ -\frac{1}{2}\exp(-y^2) \right\}y \right]_{-\infty}^{\infty} - \int_{-\infty}^{\infty} - \frac{1}{2} \exp (-y^2)\ dy \\ &=& \frac{1}{2} \int_{-\infty}^{\infty} \exp(-y^2)\ dy \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (10) \end{eqnarray}
よって、式(9)は
\begin{eqnarray} E_{ave} &=& \frac{\frac{1}{2}m n A\ v^3_{th} \frac{1}{2} }{nA\ v^2_{th}} \\ &=& \frac{1}{4} m v_{th}^2 = \frac{1}{2} k_B T \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (11) \end{eqnarray}
となる。よって、粒子の1次元の平均運動エネルギーは\( E_{ave} = \frac{1}{2} k_B T \)である。
次に、3次元\( (u,\ v,\ w) \)に拡張する。式は複雑ではあるが単純な計算であるのですぐ解ける。マクスウェル分布は確率分布であるので、 3次元に拡張する場合も確率と同様に扱えば良い。 それぞれの方向は互いに独立であるので、3次元のマクスウェル分布\( f(u,\ v,\ w) \)は
\begin{equation} f(u,\ v,\ w) = f(u)f(v)f(w) = A^3 \exp \left\{ -\frac{1}{2} \frac{m}{k_B T} \left( u^2 +v^2+ w^2 \right) \right\} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (12) \end{equation}
である。1次元の場合と同様にして、平均エネルギーを求める。3次元の場合の平均エネルギー\( E_{ave} \)は
\begin{eqnarray} E_{ave} &=& \frac{ \frac{1}{2}m n \int\int\int_{-\infty}^{\infty}(u^2 + v^2 + w^2)\ f(u,\ v,\ w)\ dudvdw} {n \int\int\int_{-\infty}^{\infty}\ f(u,\ v,\ w)\ dudvdw} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (13) \\ &=& \frac{\int_{-\infty}^{\infty} \frac{1}{2}m u^2\ n f(u)\ du}{\int_{-\infty}^{\infty} n f(u)\ du} + \frac{\int_{-\infty}^{\infty} \frac{1}{2}m v^2\ n f(v)\ dv}{\int_{-\infty}^{\infty} n f(v)\ dv} + \frac{\int_{-\infty}^{\infty} \frac{1}{2}m u^2\ n f(w)\ dw}{\int_{-\infty}^{\infty} n f(w)\ dw} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (14) \end{eqnarray}
となる。ここで、式(14)の第1項は1次元の場合の平均運動エネルギーである。 図1からわかる様にマクスウェル分布は等方的であるので、第2項も第3項も第1項と結果が同じになることに気づく。 つまり、3次元の場合の平均運動エネルギーは
\begin{equation} E_{ave} = \frac{3}{2} k_B T \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (15) \end{equation}
となるのである。これは1自由度につき\( \frac{1}{2}k_B T \)であることを示している。 このようにして、プラズマ物理ではエネルギーを温度として表す。