プラズマ

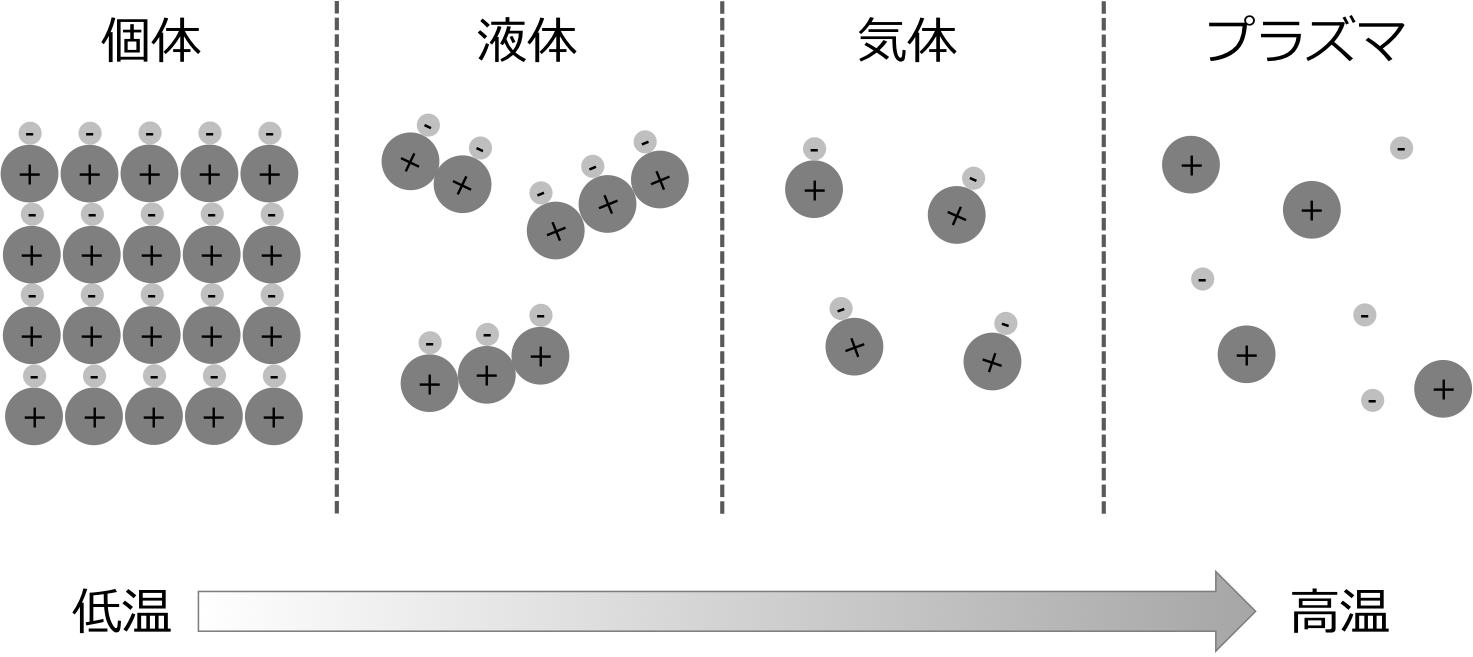
図1-1-1 物質の４態

プラズマとは何かを考える前に、物質の３態について簡単に説明する。

温度がその物質の融点より低い状態であると、物質は個体となる。 H\(_2\)Oで言えば氷の状態である。

個体ではそれぞれの分子の間に働く力が強く、分子は振動はするが、平均位置を変えることはない。図1-1-1に個体の状態を分かりやすく示してあるが、個体とは分子が整列し、密に詰まった状態のことをいう。

融点を超えると液体となる。液体は個体ほどではないが、分子間力によって、それぞれの分子がお互いに影響し合う。しかし、それぞれの分子が運動できるくらい分子間力は弱く、液体の物質は形を容易に変えることができる。 H\(_2\)Oで言うところの水である。

沸点を超えると、次は物質は気体となる。気体ではそれぞれの分子の間にはほとんど力はかからない。理想気体は、それぞれの分子の間の力は0としている。気体となった物質の分子は高速に運動をする。

では沸点を超えて温度をどんどん高くしていくと物質はどうなるのだろうか？

高速に運動する分子は互いに衝突を起こす。衝突のエネルギー（衝突で分子が失う運動エネルギー）が、分子の最外殻電子を叩き出すのに十分なエネルギーであった場合、その分子は電離される。

つまり、プラスに帯電したイオンと、マイナスに帯電した電子が別々に運動する状態になるのである。この状態のことをプラズマと呼ぶ。

プラズマとは何かを考える上で、分かりやすい公式がある。 Sahaの式（サハの式）と言う公式で、熱平衡状態にある気体の電離度を示す式である。

\begin{equation} \frac{n_i}{n_n} \approx 2.4 \times 10^{15} \frac{T^{3/2}}{n_i} e^{-U_i / k_B T}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{equation}

ここで、\( n_i \)、\( n_n \)はそれぞれイオンと中性粒子の密度（個/cm\(^{-3}\)）、\( T \)は温度、 \( U_i \)は最外殻の電子を叩き出すエネルギー（イオン化エネルギー）（erg）、\( k_B \)はボルツマン定数である。

この式はcgs単位系で記述されており、1 eV = \(1.6 \times 10^{12} \) ergである。我々が生活している環境下においては、どの程度空気が電離されうるのかをまずSahaの式で見積もってみる。

地表面の空気の数密度はおよそ、\( n_n \approx 3 \times 10^{19} \) 個/cm\(^{-3}\)、\( T \approx 300 \)Kである。空気中に最も多い窒素のイオン化エネルギーは\( U_i= 14.5 \) eVであるのでこれを採用して、sahaの式に代入して、 \( n_i \)を求めて電離度\( n_i / (n_i + n_n) \)を導出すると

\begin{equation} \frac{n_i}{(n_i + n_n)} \approx \frac{n_i}{n_n} \approx 10^{-122} \end{equation}

となり、全くと言っていいほど、自然界では大気は電離されていないのである。 \( k_B T \)が\( U_i \)より相当小さい場合は、電離度はほぼ0である。

しかし、\( k_B T \)が\( U_i \)の数分の１あたりまで上昇した時に電離度が急激に増加し、プラズマ状態になる。この時の\( T \sim 10^5 \) Kである。もっと温度が上がれば完全に電離する。このことから、極めて高温の天体内部や稲妻などにプラズマ状態が見られることがわかる。

電離されたイオンは電子と出会うことで再結合し、中性粒子に戻る。今プラズマを考えるとイオンと電子密度はほぼ等しいと考えることができて、再結合の度合いはイオンの密度によって決まる。

つまり、イオンの密度が大きければ大きいほど、再結合が進み電離度は小さくなる。このことから、sahaの式の右辺に\( n_i \)が現れているのである。