円柱座標(円筒座標)におけるベクトル演算子
カテゴリー:物理数学
ベクトル演算子の勾配(grad)、発散(div)、回転(rot)を円柱座標で実行する際には、直交座標の場合から変換を行う必要がある。
導出方法は少々複雑なので、まずは結果から示す。
円柱座標系における、勾配、発散、回転は以下のように表すことができる。
\begin{align} \nabla f &= \frac{\partial f}{\partial r} {\bf e}_r + \frac{1}{r}\frac{\partial f}{\partial \theta}{\bf e}_{\theta} + \frac{\partial f}{\partial z}{\bf e}_{z} &(1)\\ \nabla \cdot {\bf A} &= \frac{1}{r}\left[ \frac{\partial}{\partial r}\left( r A_r \right) + \frac{\partial A_{\theta}}{\partial \theta} + r \frac{\partial A_z}{\partial z}\right] &(2)\\ \nabla \times {\bf A} &= \left[ \frac{1}{r}\frac{\partial A_z}{\partial \theta} - \frac{\partial A_{\theta}}{\partial z} \right] {\bf e}_r + \left[ \frac{\partial A_r}{\partial z} - \frac{\partial A_z}{\partial r} \right]{\bf e}_{\theta} + \frac{1}{r} \left[ \frac{\partial}{\partial r}\left( rA_{\theta} \right) - \frac{\partial A_r}{\partial \theta} \right] {\bf e}_z &(3) \end{align}
これらの関係式をテストの時に毎回導出するのは時間がかかってしまうので、テストの際は問題用紙に与えられていることを願った方がいいかもしれない。
また、式(1), (2), (3)は覚えてしまってもいいが、テスト以外では調べればすぐにわかるので、解き方をある程度理解しておけば良いと思う。
以下に、導出方法を記述しておく。
直交座標系の勾配、発散、回転は
\begin{align} \nabla f &= \left( {\bf e}_x\frac{\partial}{\partial x} + {\bf e}_y\frac{\partial}{\partial y} + {\bf e}_z\frac{\partial}{\partial z} \right)f \\ &= \frac{\partial f}{\partial x}{\bf e}_x + \frac{\partial f}{\partial y}{\bf e}_y + \frac{\partial f}{\partial z}{\bf e}_z &(4) \\ \nabla \cdot {\bf A} &= \left( {\bf e}_x\frac{\partial}{\partial x} + {\bf e}_y\frac{\partial}{\partial y} + {\bf e}_z\frac{\partial}{\partial z} \right)\cdot \left( A_x{\bf e}_x + A_y{\bf e}_y + A_z{\bf e}_z \right) \\ &= \frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} &(5) \\ \nabla \times {\bf A} &= \left( {\bf e}_x\frac{\partial}{\partial x} + {\bf e}_y\frac{\partial}{\partial y} + {\bf e}_z\frac{\partial}{\partial z} \right) \times \left( A_x{\bf e}_x + A_y{\bf e}_y + A_z{\bf e}_z \right) \\ &= \left( \frac{\partial A_z}{\partial y} - \frac{\partial A_y}{\partial z} \right) {\bf e}_x + \left( \frac{\partial A_x}{\partial z} - \frac{\partial A_z}{\partial x} \right) {\bf e}_y + \left( \frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y} \right) {\bf e}_z &(6) \end{align}
と表される。
これを、\( \frac{\partial}{\partial r},\ \frac{\partial}{\partial \theta},\ \frac{\partial}{\partial z},\ \ {\bf e}_r,\ {\bf e}_{\theta},\ {\bf e}_z \)で表される系に変換する必要がある。
この時、円柱座標系と図1の場合を考えている。
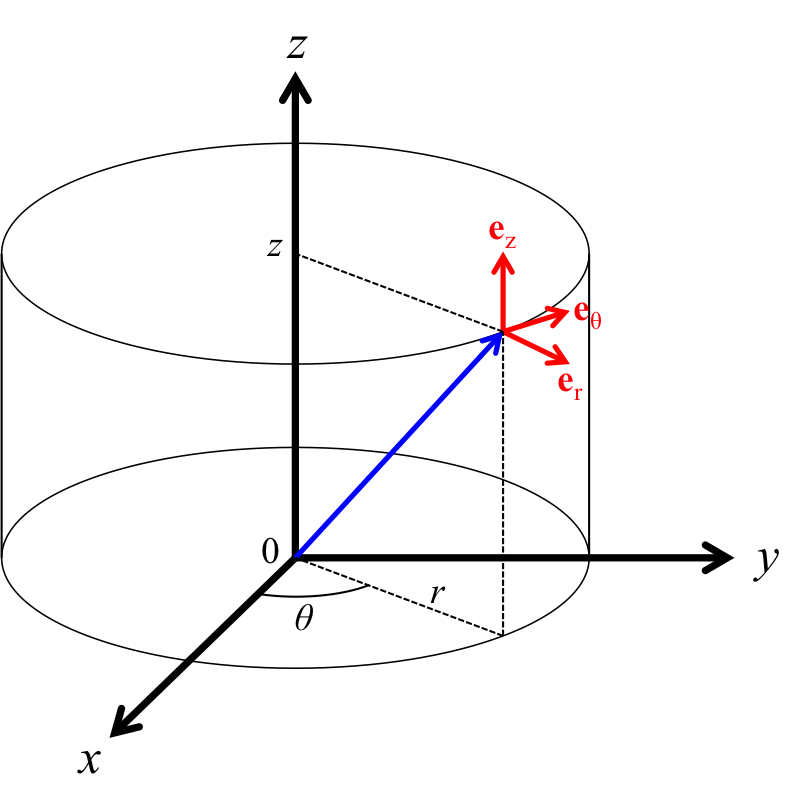
図1 円柱座標
これを見ると、\(z\)軸だけは直交座標系のままでよく、\(x,\ y\)平面だけを2次元極座標に変換してやればいいのである。
つまり、
\begin{align} x &= r \cos \theta &(7) \\ y &= r \sin \theta &(8) \\ z &= z &(9) \end{align}
である。
ではまず始めに、\( x,\ y\)の偏微分を変換する。\(x,\ y\)の偏微分は\( r,\ \theta\)の偏微分と以下のような関係式がある。
\begin{align} \frac{\partial }{\partial x} &= \frac{\partial }{\partial r}\frac{\partial r}{\partial x} + \frac{\partial }{\partial \theta}\frac{\partial \theta}{\partial x} &(10) \\ \\ \frac{\partial }{\partial y} &= \frac{\partial }{\partial r}\frac{\partial r}{\partial y} + \frac{\partial }{\partial \theta}\frac{\partial \theta}{\partial y} &(11) \end{align}
また、式(7), (8), (9)から以下の関係が導くことができる。
\begin{eqnarray} r = \sqrt{x^2 + y^2} \ \ \ \ \ \ \ \ \ (12) \\ \theta = \tan^{-1} \frac{y}{x}\ \ \ \ \ \ \ \ \ \ \ (13) \end{eqnarray}
このことから、\(x,\ y\)の偏微分は以下のように表すことができる。
\begin{align} \frac{\partial r}{\partial x} &= \frac{x}{\sqrt{x^2 + y^2}} = \frac{x}{r} = \cos \theta &(14) \\ \frac{\partial r}{\partial y} &= \frac{y}{\sqrt{x^2 + y^2}} = \frac{y}{r} = \sin \theta &(15)\\ \frac{\partial \theta}{\partial x} &= - \frac{y}{x^2} \frac{1}{1+\left( \frac{y}{x} \right)^2} = - \frac{y}{r^2} = - \frac{\sin \theta}{r} &(16)\\ \frac{\partial \theta}{\partial y} &= - \frac{1}{x} \frac{1}{1+\left( \frac{y}{x} \right)^2} = \frac{x}{r^2} = \frac{\cos \theta}{r} &(17) \end{align}
この時、\( \tan^{-1} \frac{y}{x} \)の微分に関しては、ニュートンの運動方程式の座標変換を参照にして欲しい。
式(14), (15), (16), (17)を式(10), (11)に代入することで、以下の関係式を得る。
\begin{align} \frac{\partial }{\partial x} &= \frac{\partial}{\partial r} \cos \theta - \frac{\partial}{\partial \theta} \left( \frac{\sin \theta}{r} \right) &(18) \\ \frac{\partial }{\partial y} &= \frac{\partial}{\partial r} \sin \theta + \frac{\partial}{\partial \theta} \left( \frac{\cos \theta}{r} \right) &(19) \end{align}
これで、\(\frac{\partial}{\partial x},\ \frac{\partial}{\partial y} \)を\( \frac{\partial}{\partial r},\ \frac{\partial}{\partial \theta} \)に変換する 式を得ることができた。
次に、単位ベクトルの変換をおこなっていく。
上で示したように、\( z \)軸方向は直交座標のままであるので、変換の必要はない。
\( x,\ y\)平面での単位ベクトルである、\( {\bf e}_x,\ {\bf e}_y \)のみを変換すればよいのである。
\(x,\ y\)平面における極座標の位置ベクトル\( {\bf r} \)は
\begin{eqnarray} {\bf r} = r \cos \theta {\bf e}_x + r \sin \theta {\bf e}_y \ \ \ \ \ \ \ \ (20) \end{eqnarray}
で表される。
この関係式から\( r \)方向と\( \theta \)方向の単位ベクトル\( {\bf e}_r,\ {\bf e}_{\theta} \)を求める。
単位ベクトル\( {\bf e}_r,\ {\bf e}_{\theta} \)は、以下のように求めることができる。
\begin{align} {\bf e}_r &= \frac{\frac{\partial {\bf r}}{\partial r}}{\left| \frac{\partial {\bf r}}{\partial r} \right|} &(21) \\ \\ {\bf e}_{\theta} &= \frac{\frac{\partial {\bf r}}{\partial \theta}}{\left| \frac{\partial {\bf r}}{\partial \theta} \right|} &(22) \end{align}
ここで、\( \left|\frac{\partial {\bf r}}{\partial r} \right|\)と\( \left|\frac{\partial {\bf r}}{\partial \theta} \right|\)はベクトルの大きさである。
各方向の微小変化を導き、その大きさで割ることで、ベクトルの大きさを1にしたのである。
では実際に式(21)と式(22)の計算を行うと以下の関係式を得る。
\begin{align} {\bf e}_r &= \cos \theta {\bf e}_x + \sin \theta {\bf e}_y &(23)\\ {\bf e}_{\theta} &= - \sin \theta {\bf e}_x + \cos \theta {\bf e}_y &(24) \end{align}
この式(23), (24)を連立方程式として、\( {\bf e}_x,\ {\bf e}_y \)について解くことで以下の関係式を導くことができる。
\begin{eqnarray} {\bf e}_x &=& \cos \theta {\bf e}_r - \sin \theta {\bf e}_\theta \ \ \ \ \ \ \ \ \ \ \ \ \ (25) \\ {\bf e}_y &=& \sin \theta {\bf e}_r + \cos \theta {\bf e}_\theta \ \ \ \ \ \ \ \ \ \ \ \ \ (26) \end{eqnarray}
この関係式をナブラ
\begin{eqnarray} \nabla = \left( {\bf e}_x\frac{\partial}{\partial x} + {\bf e}_y\frac{\partial}{\partial y} + {\bf e}_z\frac{\partial}{\partial z} \right)\ \ \ \ \ \ (27) \end{eqnarray}
に式(18), (19)と式(25), (26)を代入すると、
\begin{eqnarray} \nabla &= \left( \cos \theta {\bf e}_r - \sin \theta {\bf e}_\theta \right) \left\{ \frac{\partial}{\partial r} \cos \theta - \frac{\partial}{\partial \theta} \left( \frac{\sin \theta}{r} \right)\right\} + \left( \sin \theta {\bf e}_r + \cos \theta {\bf e}_\theta \right) \left\{ \frac{\partial}{\partial r} \sin \theta + \frac{\partial}{\partial \theta} \left( \frac{\cos \theta}{r} \right) \right\} + \frac{\partial}{\partial z}{\bf e}_z \ \ \ \ \ \ \ \ (28) \end{eqnarray}
を得る。
これらをまとめると、
\begin{eqnarray} \nabla = {\bf e}_r\frac{\partial}{\partial r} + {\bf e}_{\theta} \frac{1}{r} \frac{\partial}{\partial \theta} + {\bf e}_z\frac{\partial}{\partial z} \ \ \ \ \ \ \ \ \ \ (29) \end{eqnarray}円柱座標系における勾配
このナブラを求めることができたことによって勾配はすぐに、
\begin{align} \nabla f &= \frac{\partial f}{\partial r} {\bf e}_r + \frac{1}{r} \frac{\partial f}{\partial \theta} {\bf e}_{\theta} + \frac{\partial f}{\partial z}{\bf e}_z &(30) \end{align}
と求めることができる。
この時、慣例として単位ベクトルを偏微分の後ろに記述したが、単位ベクトルは微分しない。
円柱座標系における発散
発散を求める場合はもう少し計算を進める必要がある。
式(29)を使って、円柱座標の発散は
\begin{align} \nabla \cdot {\bf A} &= \left( {\bf e}_r\frac{\partial}{\partial r} + {\bf e}_{\theta} \frac{1}{r} \frac{\partial}{\partial \theta} + {\bf e}_z\frac{\partial}{\partial z} \right) \cdot \left( A_r {\bf e}_r + A_{\theta} {\bf e}_{\theta} + A_z {\bf e}_z \right) &(31) \end{align}
と表される。
この時、注意しなければならないことがある。
右辺1つ目の括弧内の単位ベクトルに偏微分を実行する必要はない。
これはナブラに方向を与える役目のみであるからである。
しかし、右辺2つ目の括弧内の単位ベクトルに偏微分は実行される。
これは、ベクトル\( {\bf A} \)の成分であるからである。
よって、単位ベクトルの微分が、
\begin{eqnarray} \frac{\partial}{\partial r} {\bf e}_r &=& 0 \\ \frac{\partial}{\partial \theta} {\bf e}_r &=& {\bf e}_{\theta} \\ \frac{\partial}{\partial z} {\bf e}_r &=& 0 \\ \frac{\partial}{\partial r} {\bf e}_{\theta} &=& 0 \\ \frac{\partial}{\partial \theta} {\bf e}_{\theta} &=& - {\bf e}_r \\ \frac{\partial}{\partial z} {\bf e}_{\theta} &=& 0 \\ \frac{\partial}{\partial r} {\bf e}_z &=& 0 \\ \frac{\partial}{\partial \theta} {\bf e}_z &=& 0 \\ \frac{\partial}{\partial z} {\bf e}_z &=& 0 \\ \end{eqnarray}
と表されることに注意して、式(31)を展開する。
\begin{eqnarray} \left( {\bf e}_r\frac{\partial}{\partial r} + {\bf e}_{\theta} \frac{1}{r} \frac{\partial}{\partial \theta} + {\bf e}_z\frac{\partial}{\partial z} \right) \cdot \left( A_r {\bf e}_r + A_{\theta} {\bf e}_{\theta} + A_z {\bf e}_z\right) = \frac{\partial}{\partial r} A_r + \frac{1}{r} \frac{\partial }{\partial\theta} A_{\theta} + \frac{1}{r}A_r + \frac{\partial}{\partial z} A_z \ \ \ \ \ \ (32) \end{eqnarray}
(単位ベクトルの2乗は1になる)式(32)を整理すると、
\begin{eqnarray} \nabla \cdot {\bf A} = \frac{1}{r} \left[ \frac{\partial}{\partial r} \left( r A_r \right) + \frac{\partial }{\partial \theta} A_{\theta} + r \frac{\partial }{\partial z}A_z \right]\ \ \ \ \ \ \ \ (33) \end{eqnarray}
を得ることができるのである。
円柱座標系における回転
では最後に回転を求めて行く。
苦労して求めてたナブラ式(32)を使って、回転を表すと以下のようになる。
\begin{eqnarray} \nabla \times {\bf A} &=& \left( {\bf e}_r\frac{\partial}{\partial r} + {\bf e}_{\theta} \frac{1}{r} \frac{\partial}{\partial \theta} + {\bf e}_z\frac{\partial}{\partial z} \right) \times \left( A_r {\bf e}_r + A_{\theta} {\bf e}_{\theta} + A_z {\bf e}_z\right)\ \ \ \ \ \ \ \ \ \ \ \ (34) \end{eqnarray}
回転の場合も同様に右辺の左側の単位ベクトルを微分する必要はないが、右辺の右側の括弧内の単位ベクトルは微分する必要がある。
これに注意して、式(34)を展開する。
\begin{align} \left( {\bf e}_r\frac{\partial}{\partial r} + {\bf e}_{\theta} \frac{1}{r} \frac{\partial}{\partial \theta} + {\bf e}_z\frac{\partial}{\partial z} \right) &\times \left( A_r {\bf e}_r + A_{\theta} {\bf e}_{\theta} + A_z {\bf e}_z\right) \\ &= {\bf e}_r \frac{\partial}{\partial r} \times \left( A_r {\bf e}_r \right) + {\bf e}_r \frac{\partial}{\partial r} \times \left( A_{\theta} {\bf e}_{\theta} \right) + {\bf e}_r \frac{\partial}{\partial r} \times \left( A_z {\bf e}_z \right) \\ &\ \ \ \ \ \ +\frac{1}{r} \left[ {\bf e}_{\theta} \frac{\partial}{\partial \theta} \times \left( A_r {\bf e}_r \right) + {\bf e}_{\theta} \frac{\partial}{\partial \theta} \times \left( A_{\theta} {\bf e}_{\theta} \right) + {\bf e}_{\theta} \frac{\partial}{\partial \theta} \times \left( A_z {\bf e}_z \right) \right]\\ &\ \ \ \ \ \ \ \ \ + {\bf e}_z \frac{\partial}{\partial z} \times \left( A_r {\bf e}_r \right) + {\bf e}_z \frac{\partial}{\partial z} \times \left( A_{\theta} {\bf e}_{\theta} \right) + {\bf e}_z \frac{\partial}{\partial z} \times \left( A_z {\bf e}_z \right) \\ \\ &= {\bf e}_r \times {\bf e}_r \frac{\partial}{\partial r} A_r + {\bf e}_r \times {\bf e}_{\theta} \frac{\partial}{\partial r} A_{\theta} + {\bf e}_r \times {\bf e}_z \frac{\partial}{\partial r}A_z \\ &\ \ \ \ \ \ + \frac{1}{r} \left[ {\bf e}_{\theta} \times {\bf e}_r \frac{\partial}{\partial \theta}A_r + {\bf e}_{\theta} \times A_r \frac{\partial}{\partial \theta} {\bf e}_r + {\bf e}_{\theta} \times {\bf e}_{\theta} \frac{\partial}{\partial \theta} A_{\theta} + {\bf e}_{\theta} \times A_{\theta} \frac{\partial}{\partial \theta} {\bf e}_{\theta} + {\bf e}_{\theta} \times {\bf e}_z \frac{\partial}{\partial \theta} A_z \right]\\ &\ \ \ \ \ \ \ \ \ \ \ \ + {\bf e}_z \times {\bf e}_r \frac{\partial}{\partial z} A_r + {\bf e}_z \times {\bf e}_{\theta} \frac{\partial}{\partial \theta} A_{\theta} + {\bf e}_z \times {\bf e}_z \frac{\partial}{\partial z}A_z\ \ \ \ \ \ \ (35) \end{align}
となる。
展開だけでも一苦労であるが、あと一息で計算は終わるので頑張る。
図1に示したように、単位ベクトルは違いに直交している。
外積を取るとき、同じ方向の単位ベクトルどうしの外積は0になり、その他の単位ベクトルどうしの外積は右ねじの法則により、
\begin{align} {\bf e}_r \times {\bf e}_{\theta} &= {\bf e}_z &(36) \\ {\bf e}_r \times {\bf e}_z &= -{\bf e}_{\theta} &(37) \\ {\bf e}_{\theta} \times {\bf e}_z &= {\bf e}_r &(38) \\ {\bf e}_{\theta} \times {\bf e}_r &= -{\bf e}_z &(39) \\ {\bf e}_z \times {\bf e}_r &= {\bf e}_{\theta} &(40) \\ {\bf e}_z \times {\bf e}_{\theta} &= - {\bf e}_r &(41) \end{align}
となることを利用して式、(35)を書き直すと、
\begin{eqnarray} \nabla \times {\bf A} &=& \left( \frac{1}{r} \frac{\partial}{\partial \theta} A_z - \frac{\partial}{\partial \theta} A_{\theta} \right) {\bf e}_r + \left( \frac{\partial}{\partial z}A_r - \frac{\partial}{\partial r}A_z \right){\bf e}_{\theta} + \left( A_{\theta} + \frac{\partial}{\partial r}A_{\theta} - \frac{1}{r}\frac{\partial}{\partial \theta}A_r \right){\bf e}_z \\ &=& \left[ \frac{1}{r} \frac{\partial}{\partial \theta} A_z - \frac{\partial}{\partial \theta} A_{\theta} \right] {\bf e}_r + \left[ \frac{\partial}{\partial z}A_r - \frac{\partial}{\partial r}A_z \right] {\bf e}_{\theta} + \frac{1}{r} \left[ \frac{\partial}{\partial r}\left(r A_{\theta} \right) - \frac{\partial}{\partial \theta}A_r \right] {\bf e}_z \end{eqnarray}
となり、円柱座標での回転を求めることができる。