ベクトルの足し算・ベクトルの引き算

カテゴリー：物理数学

これまで習ってきた四則演算（足し算・引き算・掛け算・割り算）の場合は、大きさを足し合わせたり、掛け合わせればよかった。 ベクトルの場合は、「向き」という新しい特徴が加えられるため、これまでと同じ四則演算をすることができない。

つまり、これまでのように「大きさ」だけでなく、「大きさ」と「向き」を同時に足し合わせたり、掛け合わせたりしなくてはならないのである。

ここでは、ベクトルとベクトルの足し算と引き算について説明する。

ベクトルの足し算

ベクトル\( {\bf A} \)とベクトル\( {\bf B} \)を足して得られるベクトル\( {\bf C} \)について考える。

図4.　ベクトルの足し算

\( {\bf A} \)と\( {\bf B} \)の足し算は図4に示すように\( {\bf A} \)と\( {\bf B} \)で作る平行四辺形の 対角線の\( {\bf C} \)で表される。

もっと具体的に言うと、\( {\bf A} \)の終点と\( {\bf B} \)の始点を合わせて \( {\bf A} \)の始点から\( {\bf B} \)の終点までが\( {\bf C} \)である。

この時、\( {\bf A} \)の成分を\( (x_1,\ y_1) \)、\( {\bf B} \)の成分を\( (x_2,\ y_2) \)とすると、\( {\bf C} \)の成分は、\( (x_1 + x_2,\ y_1 + y_2) \)で表される。

もちろん\( {\bf C} \)の大きさは、
\begin{eqnarray} | {\bf C} | = \sqrt{(x_1 + x_2)^2 + (y_1 + y_2)^2} \end{eqnarray}
で表される。

ベクトルの引き算

\( {\bf A} \)と\( {\bf B} \)の差\( {\bf C} \)は
\begin{equation} {\bf A} - {\bf B} = {\bf C} \end{equation}
ではあるが、\( {\bf B} \)を反転させて\( -{\bf B} \)とすることで、足し算に変換することができる（図5）。

\begin{equation} {\bf A} + (- {\bf B}) = {\bf C} \end{equation}

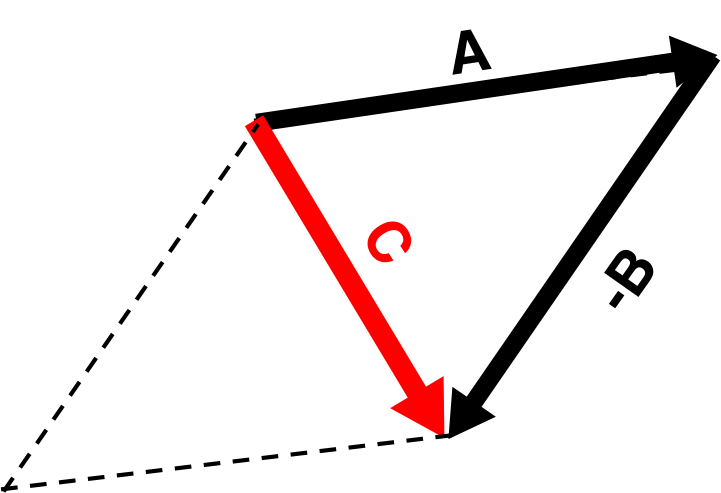
図5　ベクトルの引き算

または、ベクトルの始点同士を合わせて、

図6　ベクトルの引き算②

として、図のようにベクトルを引けば得られる。

同様にして、\( {\bf A} \)の成分を\( (x_1,\ y_1) \)、\( {\bf B} \)の成分を\( (x_2,\ y_2) \)とすると、\( {\bf C} \)の成分は、\( (x_1 - x_2,\ y_1 - y_2) \)で表され、その大きさは、 \begin{eqnarray} | {\bf C} | = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \end{eqnarray} である。

以上をまとめると

足し算の場合は、それぞれのベクトルの終点と始点を合わせて足し合わせる。

引き算の場合は、始点どうしを合わせるか、引く側のベクトルの向きを反転させて足し合わせる。

坂田アキラの　ベクトルが面白いほどわかる本 [ 坂田アキラ ] 価格：1430円（税込、送料無料) (2022/6/23時点) 楽天で購入