振り子の等時性
カテゴリー:力学
振り子の等時性とは、振り子の周期が、振れ角によらず糸の長さのみに依存するという性質である。
振り子の等時性はガリレオによって発見されており、当時は人間の脈を使って周期を計っていた。
以下に振り子の等時性の導出方法を示しておく。
図1のような振り子の角振動数\( \omega_0 \)は、振り子の振れ角\( \theta \)が非常に小さい時、
\begin{eqnarray} \omega_0 = \sqrt{\frac{g}{l}}\ \ \ \ \ \ \ (1) \end{eqnarray}
と表された。(導出方法は調和振動(単振動)のページ)
このようにして、振り子の角振動数は振り子の糸の長さ\( l \)によって決まるのである。
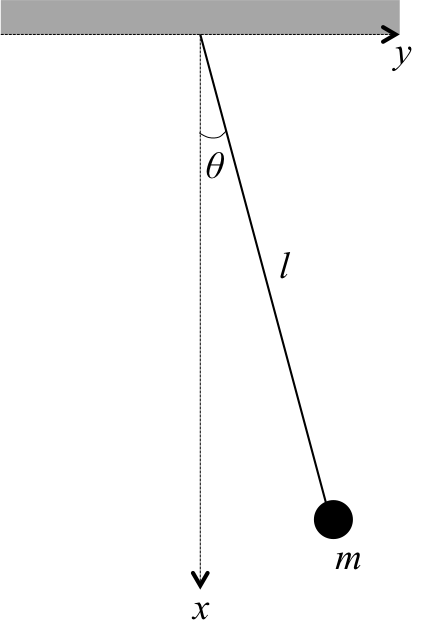
図1. 振り子
角振動数から周期\( T \)は
\begin{eqnarray} T = \frac{2 \pi}{\omega_0} = 2\pi \sqrt{\frac{l}{g}}\ \ \ \ \ \ \ (2) \end{eqnarray}
と求めることができる。
ここで、重力加速度\( g \)は、約\( 9.81 \) m/sであるので、\( \sqrt{g} = 3.13 \)となる。
この値は、円周率の\( \pi = 3.14 \)と非常に近い値である。
つまり、\( \pi \sim \sqrt{g} \)としてやることで、式(2)の振り子の周期\( T \)は、
\begin{eqnarray} T \simeq 2 \sqrt{l} \ \ \ \ \ \ \ (3) \end{eqnarray}
と近似できるのである。
式(3)から周期\( T \)は振れ角\( \theta \)に依らず糸の長さ\( l \)だけに依存することがわかる。
これが振り子の等時性である。
この場合には注意が必要である。角振動数\( \omega_0 \)を導出する際に「\(\theta\)が小さい」という仮定を置いた。
この仮定が成り立つ場合のみ、周期は糸の長さだけで周期が決まるのである。
では、どの程度の角度なら「小さい」と言えるのであろうか?
次に\( \theta \)が「小さい」と言える範囲を考えていくことにする。
等時性が成り立つθの範囲
振れ角\( \theta \)が小さい時に振り子の等時性が成り立つという制約は、この調和振動子の運動方程式を導出する際に生じている。
この振り子の運動方程式は正確には、
\begin{eqnarray} \ddot{\theta} + \frac{g}{l} \sin \theta = 0\ \ \ \ \ \ \ \ \ (4) \end{eqnarray}
と表される。
ここで、\( \ddot{\theta} \)は\( \theta \)の2階時間微分(運動方程式の加速度)、\( g \)は重力加速度、\( l \)は糸の長さである。
\( \sin \theta \)はテイラー展開できて、
\begin{eqnarray} \sin \theta = \theta - \frac{\theta^3}{6} + \frac{\theta^5}{120} - \cdots \ \ \ \ \ \ (5) \end{eqnarray}
と展開することができるのである。
この式を使って、\( \theta \)が小さい時は2項目以降が無視できるので、\( \sin \theta \sim \theta \)と近似する。
これにより、微分方程式
\begin{eqnarray} \ddot{\theta} + \frac{g}{l} \theta = 0\ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
を得ることができ、式(6)を解くことで角振動数
\begin{eqnarray} \omega_0 = \sqrt{\frac{g}{l}}\ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
を得ていたのである。
振れ角\( \theta \)が大きくなるとテイラー展開によるこの近似はもちろん使えなくなる。
では、どれくらいで振れ角を大きくしてしまうとこの近似が破られるのであろうか?
まず、振れ角を大きく見積もってみて、最大値である\( \pi / 2\)(90°)の時はどうだろうか?
第1項、第2項、第3項をそれぞれ計算してみると、
\begin{align} \theta &= 1.5708 \\ \frac{\theta^3}{6} &= 0.6460 \\ \frac{\theta^5}{120} &= 0.0797 \end{align}
となる。第2項は第1項の40%くらいの大きさの値を持っている。
これは無視することができない。一方で、第3項は振れ角最大でもそれぞれの項に比べて非常に小さい値である。
よって、第3項は振れ角90°以内では、いかなる場合でも無視することができるのである。
では、第2項が第1項に対してどれくらい大きくなると影響がでるのであろうか?
その値を決めるのは難しいのではあるが、物理の世界ではオーダー(桁)というものを非常に気にする。
例えば、「8と2」は同じ一桁なので、互いに無視することができない。
一方で、「8と0.2」の場合は8に対して0.2は無視できると考えることが多い。
このように、10分の1以下であれば無視して、10分の1以上であると無視できないと考えることが多いのである。
では、\( \sin \theta \)のテイラー展開の話に戻って、第2項が第1項の10分の1以下になる条件を探そうと思う。
これは簡単に不等式
\begin{eqnarray} \frac{\frac{\theta^3}{6}}{\theta} \lt 0.1\ \ \ \ \ \ (6) \end{eqnarray}
から求めることができて、
\begin{eqnarray} \theta \lt 0.77 \end{eqnarray}
であることがわかる。0.77ラジアンは約44°に相当する。
このことから、44°以内の振れ角であれば振り子の等時性が保証され、振り子の周期は”ほぼ”糸の長さのみに依存するのである。