調和振動（単振動）

　振り子の場合、何もしなければ重りが最下点で静止しているだけである。これは、この位置で重りにかかる重力と糸の張力が釣り合っているためである。この釣り合いの位置から糸がたるまないように少し持ち上げ、手を離すと重りは弧を描きながら釣り合いの位置に向かう。釣り合いの位置では速度が最大になり、通り過ぎてしまい、手を離した方とは反対側で同じ高さまで上がったのちにまた釣り合いの位置まで降りてくる。空気抵抗によって重りの速度が0になるまでこの運動は続く。この繰り返しの運動を振動と呼ぶ。振動は、釣り合いの位置から離れることで重力による位置エネルギーが増し、手を離すとその位置エネルギーが運動エネルギーに変換されるために起こる運動である。このように、釣り合いの位置（中心）からの距離に比例した力を受ける振動を調和振動、または単振動と呼ぶ。また、調和振動をしている系（この場合は振り子全体）を調和振動子と呼ぶ。振り子の他に調和振動子として有名なものに、ばねが挙げられる。

調和振動子
　では調和振動がどのような数式で表されるのか見ていこうと思う。図1のような振り子（調和振動子）を考える。振り子の質量は\( m \)、糸の長さは\( l \)、鉛直方向に\( x \)軸を取り、下向きを正とする。ラグランジュ方程式を使った運動方程式の導出のために、まずは運動エネルギーから導出する。振り子の運動エネルギー\( T \)は \begin{align} T &= \frac{1}{2} m \left( \frac{d l}{dt} \right)^2 \\ &= \frac{1}{2} m l^2 \dot{\theta}^2 \ \ \ \ \ \ \ \ (1) \end{align} となる。振り子の運動方程式の詳しい導出方法は、2次元極座標におけるラグラジアンの求め方を参考にして欲しい。この時、糸の長さ\( l \)は変化しないので、\( \dot{l}=0 \)となることに注意する。

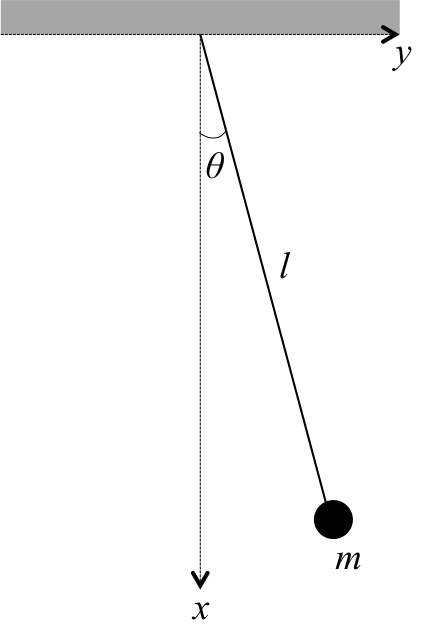
図1. 振り子

次にポテンシャルエネルギーを求めていく。ポテンシャルエネルギーは重りを持ち上げるほど（\(x\)が小さくなるほど）、大きくなる。糸がつけられている点を原点と考えると、\( x \)軸と重りをつけた糸とのなす角\( \theta \)を使って、ポテンシャルエネルギー\( U \)は \begin{eqnarray} U = - mgl\cos \theta\ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} となる。これらにより、ラグラジアン\( \cal{L} \)は、 \begin{align} \cal {L} &= T - U \\ &= \frac{1}{2} m l^2 \dot{\theta}^2 + mgl\cos \theta \ \ \ \ \ \ \ \ (3) \end{align} と求められる。式(3)のラグラジアンを、ラグランジュ方程式 \begin{eqnarray} \frac{d}{dt} \left( \frac{d}{d \dot{\theta}}{\cal L} \right) = \frac{d}{d \theta}{\cal L}\ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray} に代入することで、運動方程式 \begin{eqnarray} \ddot{\theta} + \frac{g}{l} \sin \theta = 0\ \ \ \ \ \ \ \ \ (5) \end{eqnarray} を得るのである。この時、\( \sin \theta \)をテイラー展開すると、 \begin{eqnarray} \sin \theta = \theta - \frac{\theta^3}{6} + \frac{\theta^5}{120} - \cdots \ \ \ \ \ \ (6) \end{eqnarray} と表される。もし、\( \theta \)が小さかった時は、式(6)の第2項以降は非常に小さくなるので、無視できる。つまり、\( \sin \theta \sim \theta \)と近似できる。よって、式(5)は書き換えられて、 \begin{eqnarray} \ddot{\theta} + \frac{g}{l} \theta = 0\ \ \ \ \ \ \ \ \ (6) \end{eqnarray} となる。このように微分方程式の形にすることができる。この解は三角関数で表すことができて、 \begin{eqnarray} \theta = A \sin ( \omega_0 t + \delta ) \ \ \ \ \ \ \ (7) \end{eqnarray} となる。ここで、\( \delta \)、\( A \)はそれぞれ振幅と位相で初期条件で決まるパラメーターである。また、\( \omega_0 \)は \begin{eqnarray} \omega_0^2 = \frac{g}{l} \ \ \ \ \ \ \ (8) \end{eqnarray} で表され、角振動数と呼ばれる。このように角振動数を持ち、式(7)のように周期的な変動を持つ系を調和振動子と言うのである。尚、式(7)の詳しい導出方法は微分方程式による振動の解き方のページを参照して欲しい。