ラグラジアンの求め方:2次元極座標
カテゴリー:力学
ある物体の運動エネルギーとのその位置でのポテンシャルエネルギーが分かれば、 それらからラグラジアンを求め、ラグランジュ方程式に代入することで、運動方程式を求めることができる。
ここでは極座標において、運動方程式からラグラジアンを求める方法を紹介する。 直交座標系で運動エネルギー\( T\)は
\begin{eqnarray} T = \frac{1}{2}m v^2 = \frac{1}{2}m(\dot{x}^2 + \dot{y}^2)\ \ \ \ \ \ \ \ (1) \end{eqnarray}
であるので、ここに\( x=r\cos\theta\)、\(y=r\sin\theta\)を微分し、代入することで、極座標系での運動エネルギーを求めることができる。
しかし、ここではもっと簡単な方法があるので紹介したいと思う。 図1のように点Aから点Bまで微小時間に運動する物体を考える。 ここで、微小時間の運動であるので、点Aから点Bまでの距離も非常に短いとする。 この時、点Aから点Bまでのベクトルを線要素と言い、図では\( d {\bf l} \)(青字)と表す。
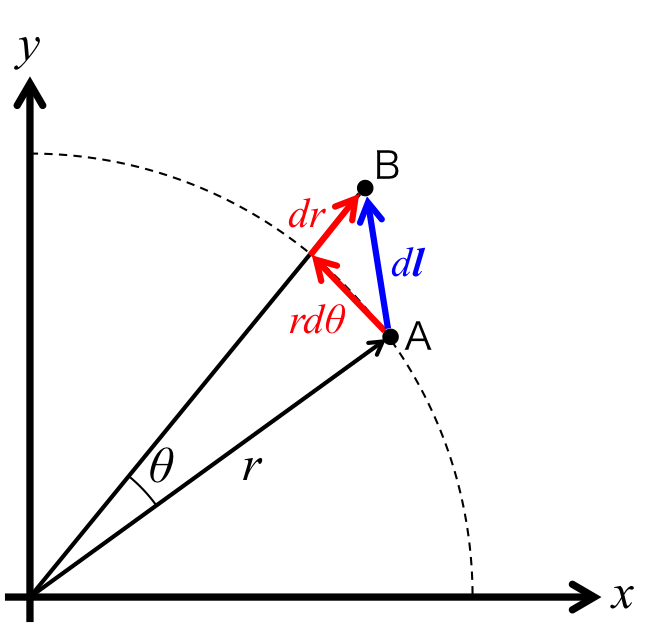
図1 極座標で点Aから点Bまで運動する物体
線要素\( d {\bf l} \)は微小時間に運動した微小距離であるので、速度との関係は
\begin{eqnarray} v = \frac{d {\bf l}}{dt}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
となる。つまり、運動方程式は
\begin{eqnarray} T = \frac{1}{2} m v^2 = \frac{1}{2}m \left( \frac{d {\bf l}}{dt} \right)^2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
と書けるのである。よって、線要素は極座標でどのように表されるのかがわかれば、すぐに運動エネルギーがわかるのである。
図1から点Bは点Aより角度を\( \theta \)だけ増加し、原点からの距離を\( dr \)だけ増加させている。
つまり、\( r\)方向には\( dr \)だけ進み、\( \theta \)方向(半径\(r\)円の円弧上)に\( r \theta \)だけ進んだことを意味している。
ここで、微小距離であるので円弧は直線にほとんど等しいとした。 これをベクトルで表すと、
\begin{eqnarray} d {\bf l} = dr {\bf e}_r + rd\theta {\bf e}_{\theta}\ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
となる。ここで、\({\bf e}_r,\ {\bf e}_{\theta}\)はそれぞれ、\(r\)方向、\( \theta \)方向の単位ベクトルである。
これは、\( dr \)と\( r d\theta\)がスカラー量であるため、ベクトル表記にするためには方向を単位ベクトルで決める必要があるからである。
では、式(3)を微分し二乗すれば、速度の2乗が得られるのだが、ここで一つ注意しなければならないことがある。
式(3)はベクトルであるので、両辺を二乗してはならない。なぜならベクトルの2乗は距離を意味するので、 両辺を2乗するのではなくて、各項を2乗する必要がある(三平方の定理)。つまり、
\begin{eqnarray} \left( \frac{d {\bf l}}{dt} \right)^2 = \dot{r}^2 + r^2\dot{\theta}^2\ \ \ \ \ \ \ \ \ (4) \end{eqnarray}
である。よって、極座標における運動エネルギーは
\begin{eqnarray} T &=& \frac{1}{2} m v^2 = \frac{1}{2}m \left( \frac{d {\bf l}}{dt} \right)^2 \\ &=& \frac{1}{2}m \left( \dot{r}^2 + r^2\dot{\theta}^2 \right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
である。このようにして導出した運動エネルギー\( T \)とポテンシャルエネルギー\( U\)から、ラグラジアン\( {\cal L} \)を
\begin{eqnarray} {\cal L} = T- U = \frac{1}{2}m \left( \dot{r}^2 + r^2\dot{\theta}^2 \right) - U\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
と求めることができるのである。線要素という考え方は非常に便利なので、頭の片隅に置いておくと良いと思う。