ラグラジアンの求め方:円筒座標
カテゴリー:力学
円筒座標は、\(x,\ y\)平面は極座標で表示され、\(z\)軸方向は通常の直交座標と同じ座標である。 らせん運動を取り扱う場合などによく用いられる座標系である。
円筒座標系は\(r, \theta, z\)で表される。ここで、直交座標系\(x,\ y,\ z\)との関係は、
\begin{eqnarray} x &=& r\cos\theta \\ y &=& r\sin\theta \\ z &=& z \end{eqnarray}
である。これらを時間で微分すると速度を得られる。
\begin{eqnarray} \dot{x} &=& \dot{r}\cos\theta - r\dot{\theta}\sin\theta \ \ \ \ \ \ \ \ (1) \\ \dot{y} &=& \dot{r}\sin\theta + r\dot{\theta}\cos\theta \ \ \ \ \ \ \ \ (2) \\ \dot{z} &=& \dot{z} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
これで、直交座標系と円筒座標系の速度の関係式が得られた。
次に、直交座標系の運動エネルギー\(T\)は
\begin{eqnarray} T= \frac{1}{2}m (\dot{x}^2 + \dot{y}^2 + \dot{z}^2)\ \ \ \ \ \ \ \ \ \ \ (4)
\end{eqnarray}
で表されるので、式(1), (2), (3)を式(4)に代入することで円筒座標での運動エネルギー\( T\)を求めることができる。よって、
\begin{eqnarray} T &=& \frac{1}{2} m \left\{ (\dot{r}\cos\theta - r\dot{\theta}\sin\theta)^2 + (\dot{r}\sin\theta + r\dot{\theta}\cos\theta)^2 + \dot{z}^2 \right\} \\ &=& \frac{1}{2} m \left\{ \dot{r}^2 \left( \sin^2\theta + \cos^2\theta \right) + r^2\dot{\theta}^2\left( \cos^2\theta + \sin^2\theta \right) + \dot{z}^2 \right\} \\ &=& \frac{1}{2} m \left( \dot{r}^2 + r^2\dot{\theta}^2 + \dot{z}^2 \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
と導くことができる。
よって、円筒座標のラグラジアン\( {\cal L} \)は、
\begin{eqnarray} {\cal L} &=& T-U \\ &=& \frac{1}{2} m \left( \dot{r}^2 + r^2\dot{\theta}^2 + \dot{z}^2 \right) - U\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
であることがわかるのである。
線要素から運動エネルギーを求める。
ここでは、微小時間に移動する距離のベクトルを表す、線要素という考え方を使ってラグラジアンを求めてみる。 線要素\( {\bf l} \)は微小時間に動くベクトルであるから、
\begin{eqnarray} d{\bf l} = dr {\bf e}_r + rd\theta {\bf e}_{\theta} + dz {\bf e}_z\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}
とできる。ここで、\({\bf e}_r,\ {\bf e}_{\theta},\ {\bf e}_z\)は\( r,\ \theta,\ z\)方向の単位ベクトルである(図1参照)。
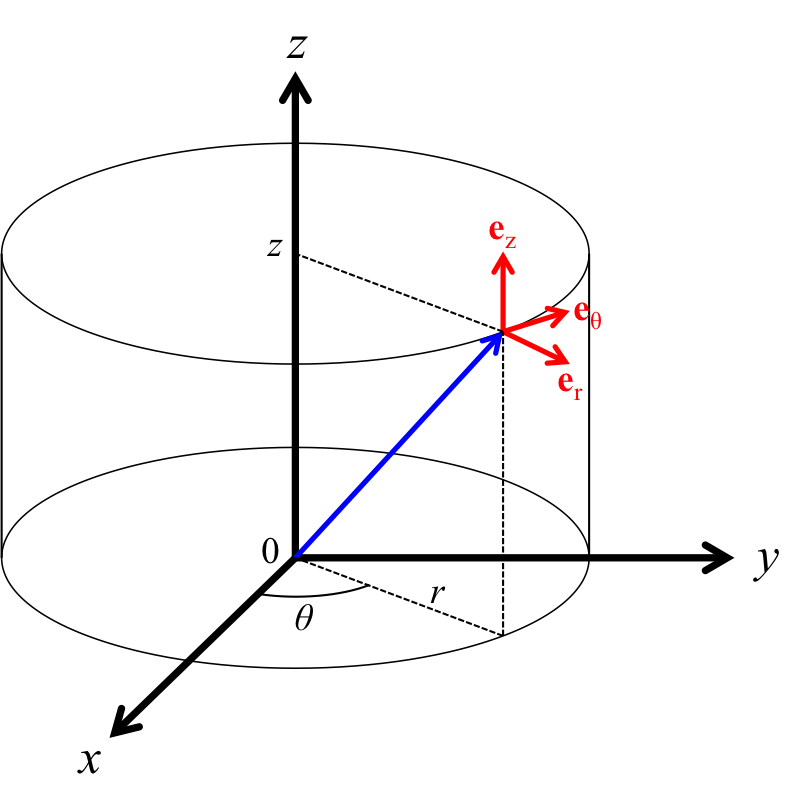
図1 円筒座標
式(7)を微分し、速度成分の各項を2乗をすると、\begin{eqnarray} \left( \frac{d{\bf l}}{dt} \right)^2= \left( \frac{dr}{dt} \right)^2 + \left( r \frac{d\theta}{dt} \right)^2 + \left( \frac{dz}{dt} \right)^2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray}
となる。ここで、式(7)の両辺を2乗するのではなく、各成分の速度成分を二乗して足し合わせる。
ベクトルの大きさを求めているので、三平方の定理を使っているのである。 これにより、速度の2乗\( v^2 \)は線要素の時間微分の二乗に等しいので、
\begin{eqnarray} v^2 = \left( \frac{d{\bf l}}{dt} \right)^2= \dot{r}^2 + \left( r \dot{\theta} \right)^2 + \dot{z}^2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray}
の関係が導ける。
よって、運動エネルギー\(T\)は
\begin{eqnarray} T &=& \frac{1}{2} m \left( \dot{r}^2 + r^2\dot{\theta}^2 + \dot{z}^2 \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (10) \end{eqnarray}
と得られるのである。この式(10)は式(5)と同じ値が得られていることがわかるだろう。
このように線要素を考えることで、難しい計算をすることなく運動エネルギーを導けるのである。