速度に依存する力:空気抵抗と終端速度
カテゴリー:力学
雨雲は、地上から2 km~5 kmくらいの所に位置していて、そこから水滴(雨粒)を降らせる。
高校の時に習った方程式に代入して地上付近での水滴の速度を求めてみよう。
地上までの到達時間\( t \)は、重力加速度を\( g \)、高度を\( h \)としたときに、
\begin{eqnarray} h = \frac{1}{2} g t^2\ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
より、
\begin{eqnarray} t = \sqrt{\frac{2h}{g}}\ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
から得られる。
雨雲の高度を3 km(3000 m)とすると\( h = 3000\ \mathrm{m} \)となり、重力加速度\( g = 9.8 \mathrm{m/s^2} \)と共に式(2)に代入すると、 \( t = 24.7 \)を得る。
つまり、雲から24.7秒で地上に到達するのである。
その時の速度は
\begin{eqnarray} v = g t = 242\ \ \mathrm{m/s} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
である。これは時速に直すと、約時速870 kmである。ものすごく早い。
拳銃の銃弾の初速が時速約1000 kmだから、銃弾と同じくらい早いことになる。
もう少し高いところで水滴が作られていれば、銃弾と同じくらいの速さになるだろう。
でも実際にはそんな速度で雨が降り注いでいないことは直感的にわかる。雨によって、撃ち抜かれたなんて話は聞いたことがない。
おおよそ見当が付いていると思うが、雨の速度を遅くしている原因は、空気抵抗である。
空気中を運動する物質は空気抵抗を受け、その力は速度によって変わる。
つまり、速度が早ければ早いほど、強い空気抵抗を受けるのである。

図1 水滴にかかる力
図11に水滴にかかる力を示した。水滴は重力により下向きに引っ張られ、下向きの加速度と速度を持つ。
この時、空気抵抗はその反対向きである上向きの力を水滴に加えて、上向きの加速度を与えることにより、水滴の速度を減らそうとする。
水滴の大きさによって空気抵抗の働き方は異なるので注意が必要だが、ここでは、水滴にかかる空気抵抗としてよく使われる速度に比例する空気抵抗\( kv \)を考える。
この水滴の運動方程式は以下のように書くことができる。
\begin{eqnarray} m a = mg - kv\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}
である。ここで、\(a \)は加速度、\( m \)は水滴の質量である。
加速度\( a \)は速度の微分で表されるので\( a = dv/dt \)である。
よって、式(4)を微分方程式として解く。 この方程式は1階の非同次微分方程式か変数分離系で解くことが有効である。
ここでは、式(4)を非同次微分方程式として解いて行く。
まず、式(4)を微分方程式とした場合の係数である\( mg \)を0とすることで、得られる一般解を求めなくてはならない。
一般解は
\begin{eqnarray} \frac{dv}{dt} = - \frac{k}{m} v \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
より、
\begin{eqnarray} v = Ce^{-\frac{k}{m}t}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
となる。ここで、\( C \)は定数である。次に\( C\)が時間に依存するとして、式(6)を元の式(1)に代入することで、
\begin{eqnarray} \frac{d}{dt} C = g e^{\frac{k}{m}t}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray}
を得る。この式(7)を積分することで、
\begin{eqnarray} C = \frac{mg}{k} e^{\frac{k}{m}t} + C_2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray}
を得る。ここで、\(C_2\)は積分定数である。この係数\(C\)を式(6)に戻してやることで
\begin{eqnarray} v = \frac{mg}{k} + C_2 e^{- \frac{k}{m}t} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray}
となる。この時、初期条件\( t=0 \)で\( v=0 \)を使って\(C_2 = - \frac{mg}{k}\)であることを求め、式(9)に代入することで、速度の時間変化の式、
\begin{eqnarray} v = \frac{mg}{k}\left( 1 - e^{- \frac{k}{m}t}\right) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (10) \end{eqnarray}
と導くことができる。この式を少し観察すると、\( t \rightarrow \infty \)で\( v = \frac{mg}{k} \)となることがわかる。
速度の時間変化式(10)を図にしてみると以下のようになる。
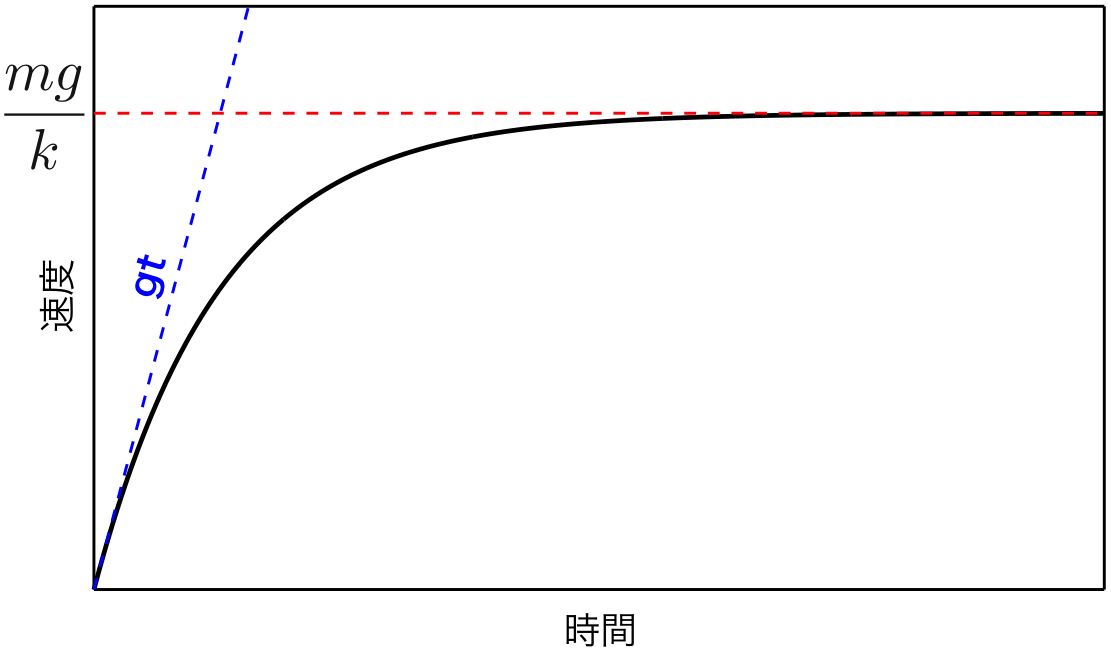
図2 空気抵抗を受ける水滴
この図から、落下直後の水滴は空気抵抗がない場合の速度である\(gt\)と同じ速度変化を見せるが、その後はすぐに空気抵抗によって速度の増加が抑えられ、 やがてある一定の値に収束することがわかる。
この速さが一定になった時の速度を終端速度と呼ぶ。
実は終端速度は重力と空気抵抗が釣り合った状態である(等速直線運動をするので、加速度は0)。
つまり運動方程式を
\begin{eqnarray} 0 = mg - kv\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (11) \end{eqnarray}
として解くことで、すぐに終端速度\( v_t\)を
\begin{eqnarray} v_t = \frac{mg}{k}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (12) \end{eqnarray}
と求めることができるのである。