等速直線運動

カテゴリー：力学

等速直線運動はすべての運動の中で最も基本的な運動である。

等速直線運動とは物体が方向を変えず一定の速度で真っすぐ進む運動のことである。

つまり、速度一定で加速度0の運動である。

例えば、西に時速100 kmで等速直線運動をしたとすると、1時間後には原点から西に丁度100 kmのところにいることになる。

この「等速直線運動」と言う言葉が入っていないと、1時間後に西に100 kmのところにいたとしても、速度まではわからないのである。

例えば、物体Aは西向きに時速100 kmで等速直線運動をし、物体Bは30分間停止し、その後時速200 kmで西向きに向かったとする。

すると、1時間後には物体A, 物体Bともに西に100 kmの位置にいる。

しかし、物体Aは常に時速100 kmで運動していたが、物体Bは時速0 kmと時速200 kmで運動していたことになる。

このように等速直線運動をしている物体はどの時刻に見てもその速度と進む方向は変わらないのである。

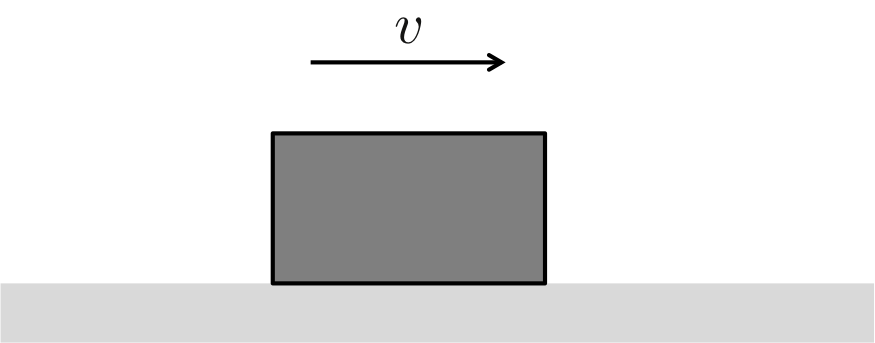
図1 速度\( v \)で等速直線運動する物体

図1のように右向きに速度\( v \)で等速直線運動をしている物体を考える。

この時、速度はいつでも\( v \)であるのでこの物体が加速することはない。

言い換えると、ニュートンの運動３法則の第１原則から等速直線運動している物体は外部から力を加えられない限り常に等速直線運動をし続けるのである。

つまり、加速度を\( a \)とすると、

である。ここで、加速度は単位時間あたりの速度の変化量であるので、速度の微分で与えられる。

速度は単位時間あたりの位置の変化量であるので、位置の微分で与えられる。

つまり、加速度は位置の２階微分で与えられることを示した。

( a= 0 \)を運動方程式\( F = ma\)に代入することで、

である。等速直線運動する物体には加速度と力が加えられていないという事実は、シンプルではあるがかなり重要なことである。

ちなみに、\( F= 0 \)は物体に全く力がかかっていないと言う意味ではなく、正確には 「力が加えられていないか、加えられている力が釣り合っており、物体にかかる合力が0」と言う意味である。

よって、力が加えられていても、それを打ち消す力が逆方向に加えられていれば、物体は等速直線運動をするのである。