三角形の重心

カテゴリー：数学A

三角形の頂点からその対辺のちょうど真ん中（中点）を結ぶ直線のことを中線と呼ぶ。 三角形のそれぞれの角とその対辺の中線は以下の様な性質がある。

三角形の3つの中線は1点で交わり、その点は各中線を2:1に内分し、重心と呼ばれる。

重心を図で示すと図1のOである。

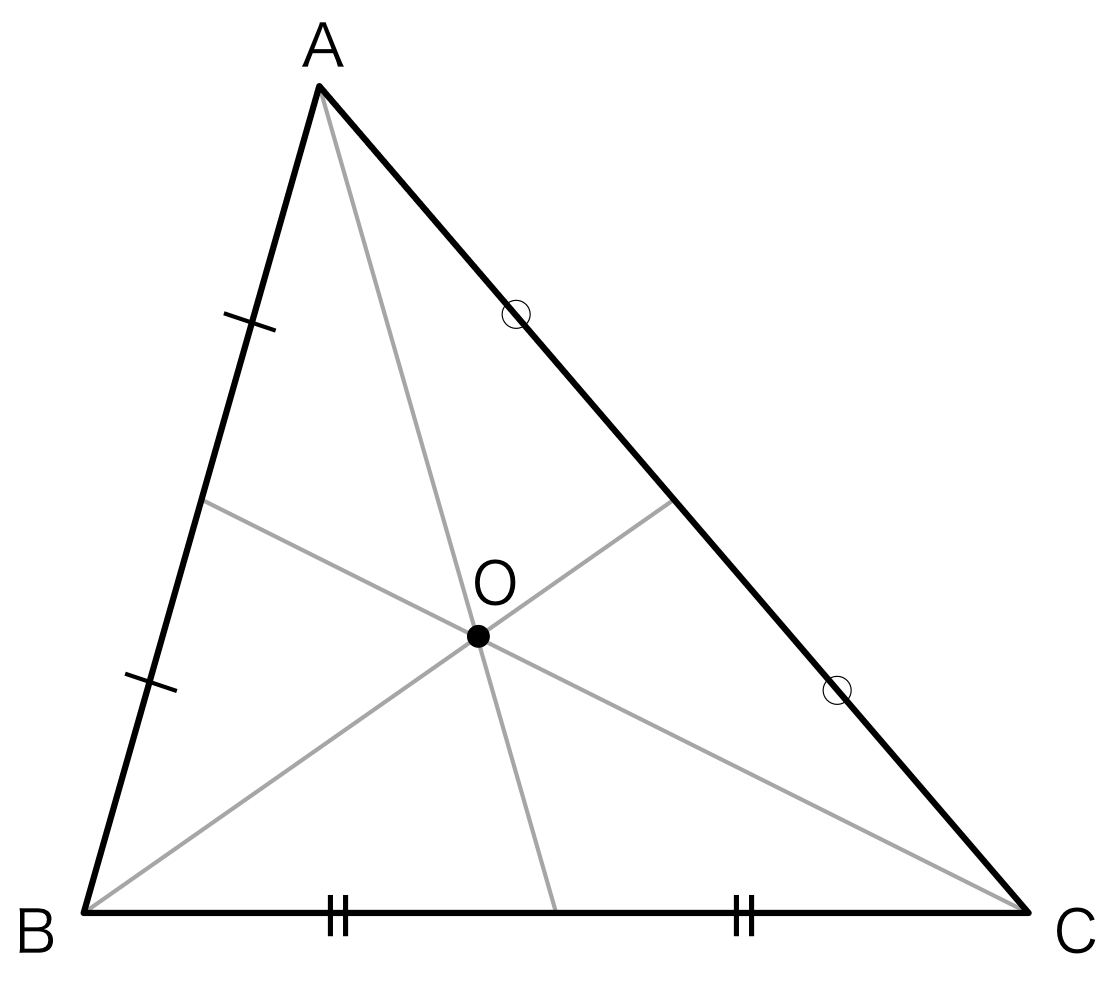
図1.

重心は数学の分野だけでなく、物理の分野でも重要な意味を持つ。

例えば、三角形のある辺の1点に糸をくくりつける。 すると、必ず糸を付けた点の真下に重心がくるのである。 また、三角形を空中に回転させながら投げると、重心を中心として三角形は回転しながら飛んでいく。

では、本題に戻って重心がそれぞれの中線を2:1に内分することを証明する。

図2のような青の2つの三角形を考える。 点Mと点Lは辺AB, 辺BCの中点であるので、2ML=ACの関係にある。 つまり、

の関係にある。

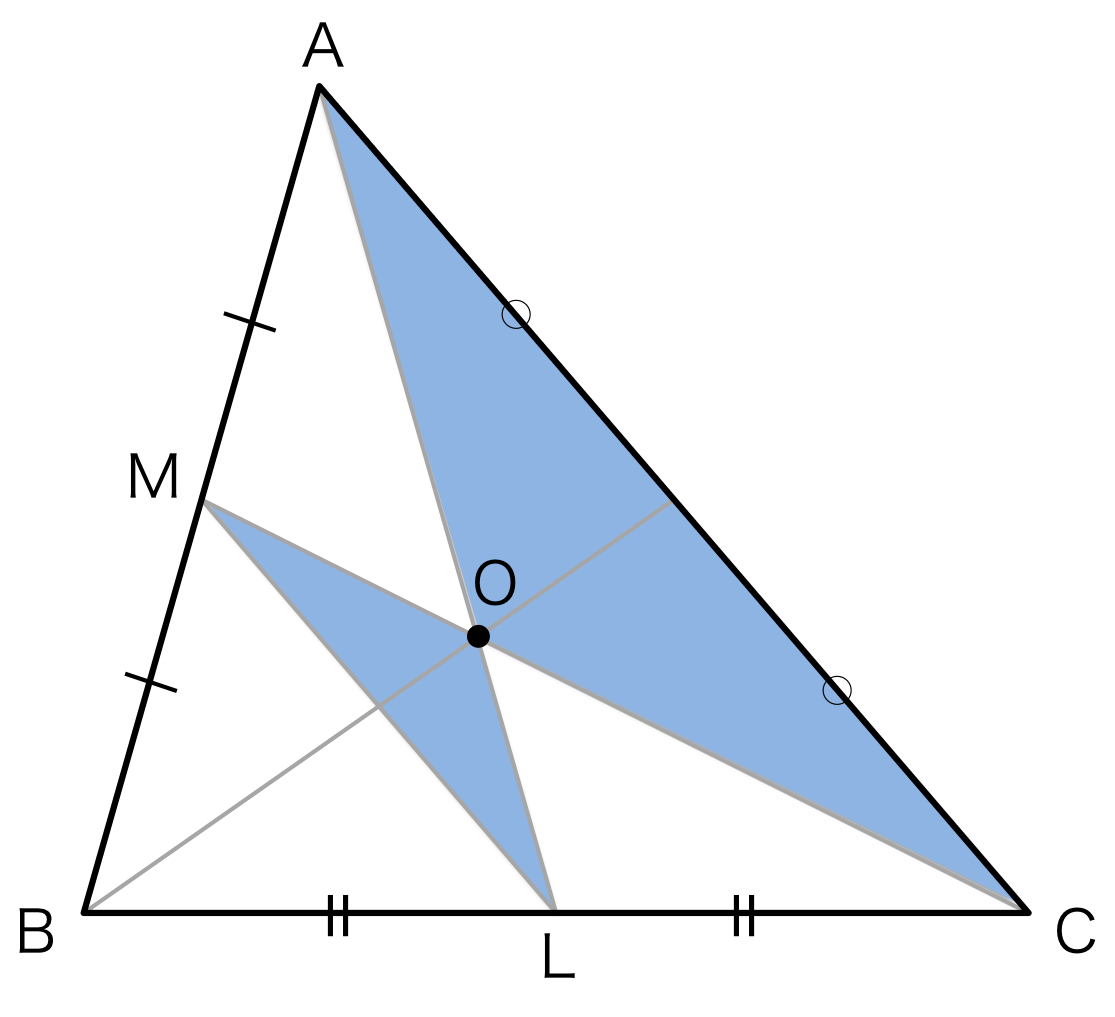
図2.

同様にして、図3のような緑の三角形を考える。 点Nと点Lは辺ACと辺BCの中点であるので、2NL=ABの関係がある。

図3.

以上から、

AO’ : LO’ = BO’ : NO’ = 2:1

の関係が導ける。このことから、点Oと点O’どちらの場合も線分ALを2:1に内分する点であることから、 点Oと点O’は一致する。 よって、それぞれの中線は1点で交わり、その点は中線を2:1に内分するのである。