三角形の内心

カテゴリー：数学A

内心から各辺まで伸ばした線は各辺と垂直に交わる。これは図1の青線で示す。

この時、\( \triangle{APO} \)と\( \triangle{ARO} \)に注目する。 \( AO \)は\( \angle A \)の二等分線なので、

\begin{eqnarray} \angle PAO = \angle RAO \end{eqnarray}

である。また、

\begin{eqnarray} \angle APO = \angle AOR = 90^{\circ} \end{eqnarray}

である。辺\( AO \)は互いに共有している。よって、1辺とその両端の角が等しいので、\( \triangle{APO} \)と\( \triangle{ARO} \)は合同である。よって、

\begin{eqnarray} OP = OR \end{eqnarray}

である。同様にして、

\begin{eqnarray} OQ = OR \end{eqnarray}

であることを示すことができる。つまり、

\begin{eqnarray} OP= OR = OQ \end{eqnarray}

を証明することができる。

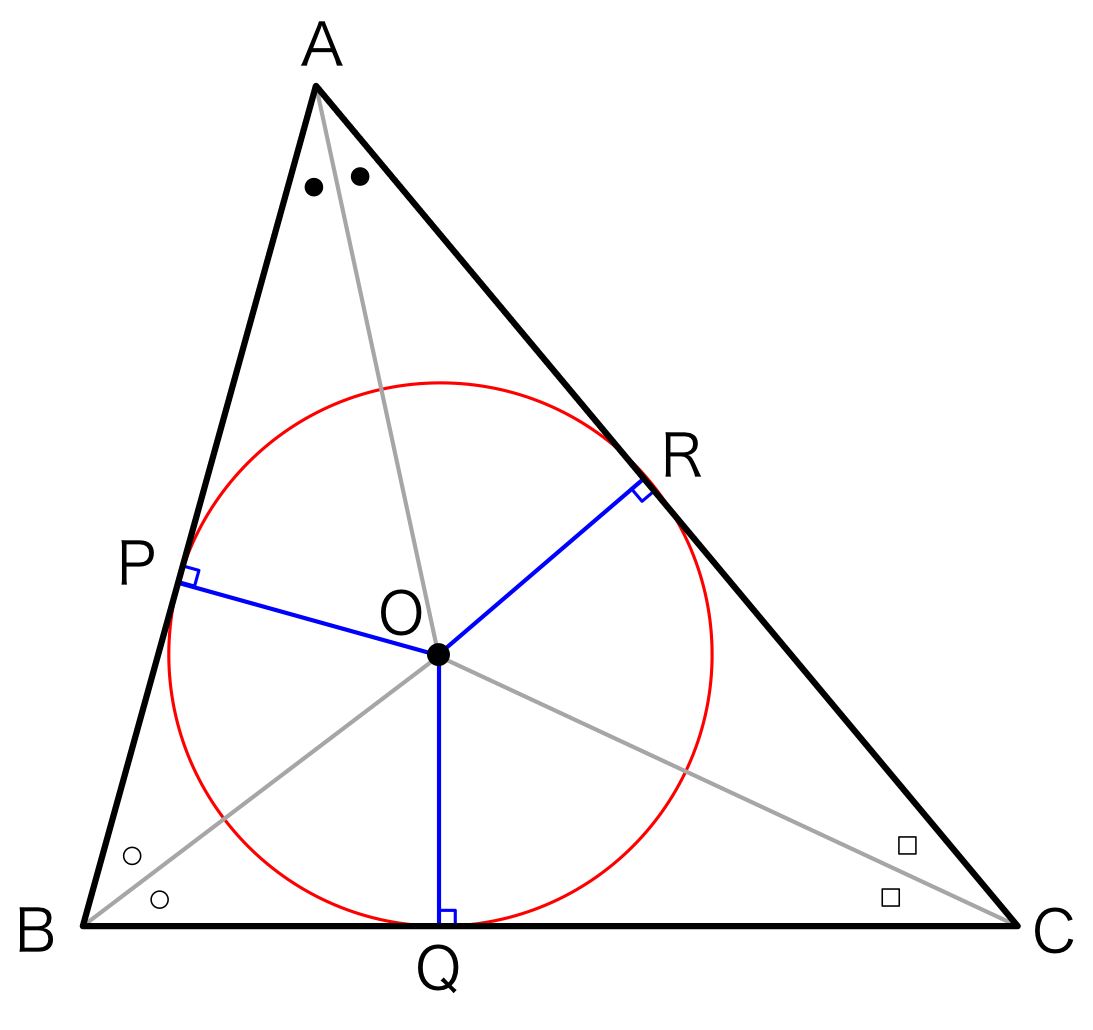
図2.

また、内心は各辺までの距離が等しい。つまり図2の赤の円のような三角形の内部に全ての辺に接する円の中心であることがわかる。この円のことを内接円と呼ぶ。