三角形の垂心

カテゴリー：数学A

図1のように三角形の各頂点から対辺に対して垂直に下ろした垂線の交点\( O \)は一点で交わる。この交点のことを垂心（すいしん）と呼ぶ。

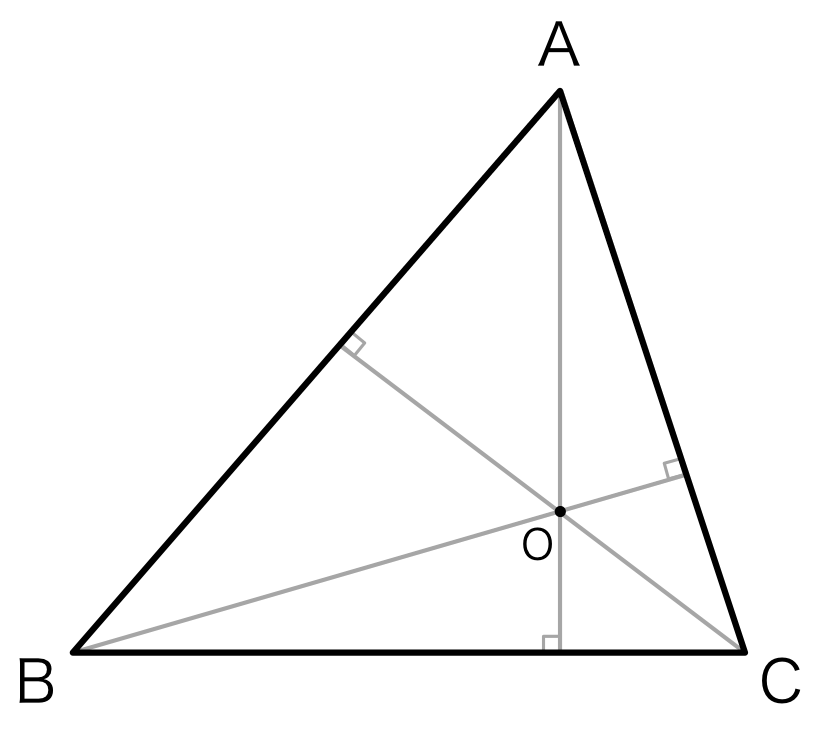
図1.

垂心は外心、重心と一直線上に位置する。また、直角三角形の垂心は直角である頂点であり、鈍角三角形の垂心は三角形の外部に位置するのである。

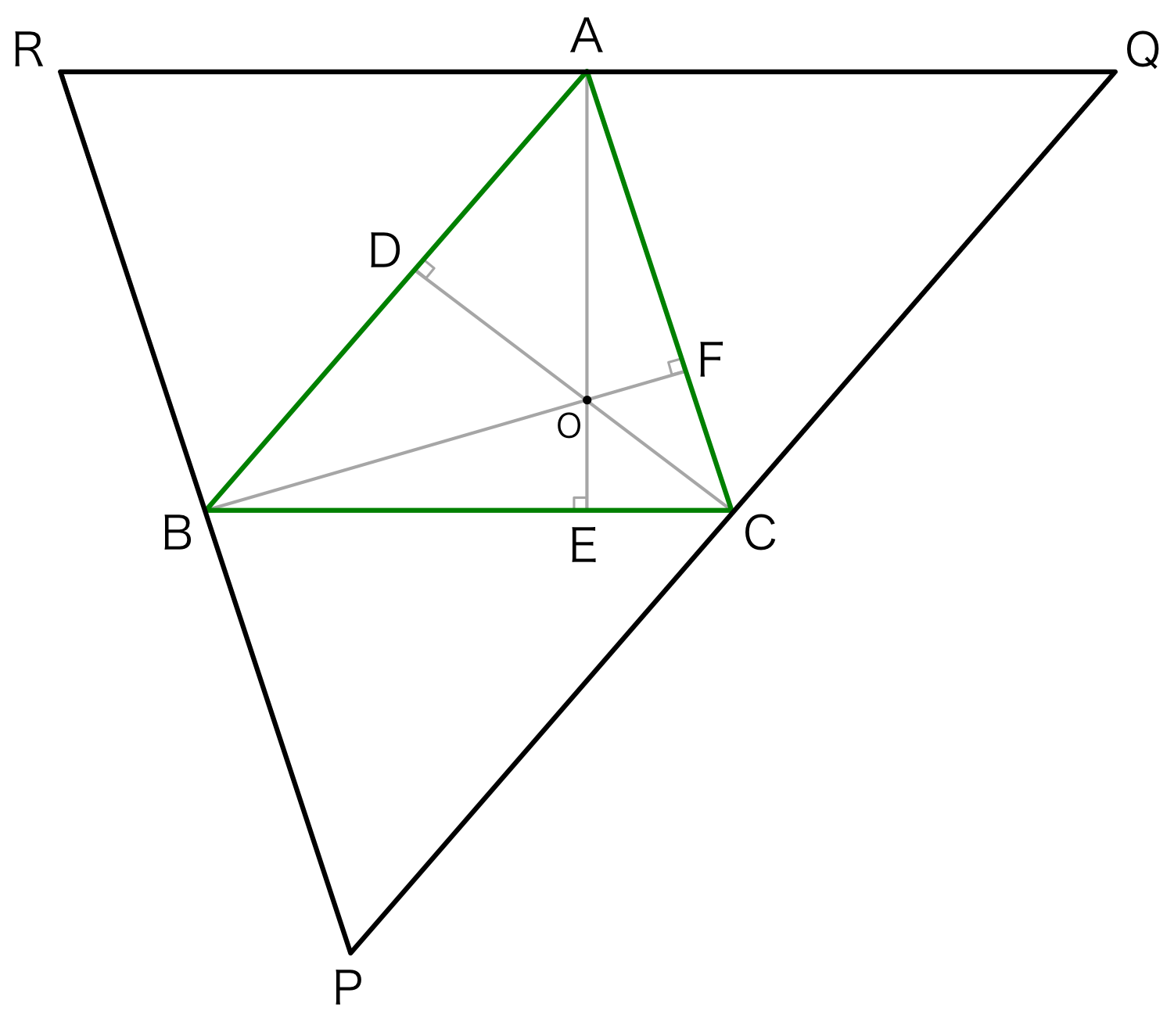
図2.

　ではここで、各頂点から対辺に対して垂直に下ろした垂直線が1点で交わることを証明する。

　図のように各頂点を通り、対辺に平行な直線を引く。この直線によってつくられる三角形を\( \triangle{PQR} \)とする。 \( AQ \parallel BC \)であるので、

\begin{eqnarray} \angle EAQ = \angle AEC = 90^{\circ} \end{eqnarray}

である。同様に、

\begin{eqnarray} \angle DCQ = \angle ADC = 90^{\circ} \\ \angle FBR = \angle AFB = 90^{\circ} \\ \end{eqnarray}

である。また、四角形ABCQは平行四辺形であるので、AQ = BCである。さらに、四角形RACBも平行四辺形であるので、RA=BCである。よって、AQ = RAである。同様にして、QC = PC、RB= BPである。

すると、点A、B、Cは\( \triangle{PQR} \)の各辺の中点であり、DC, BF, AEは各辺の垂直二等分線である。よって、点Oは\( \triangle{PQR} \)の外心である。以上より、各頂点から対辺に対して垂直に下ろした垂直線が1点で交わることが証明できる。