三角形の外心

カテゴリー：数学A

三角形の各辺の垂直二等分線に関して以下の定理が成り立つ。

　三角形の3つの辺の垂直二等分線は1点で交わり、その交点は3つの頂点から等距離にある。

これは一体どう意味であろうか？ 実際に証明をしながら説明していこうと思う。

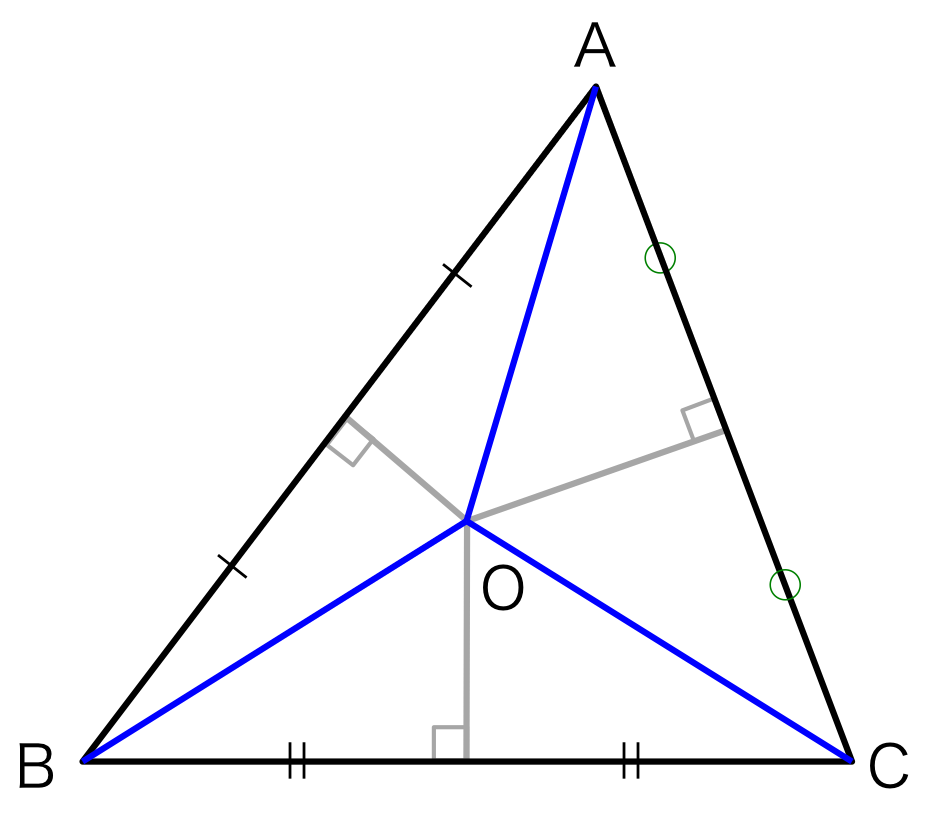
図1.

上の定理を図で表すと次の図のようになる。

この時、青で示された線分は全て同じ長さになる、ということを言っているのである。 証明は簡単である。

各辺からの垂直二等分線であるので、\( \triangle{AOB},\ \triangle{AOC},\ \triangle{BOC} \)はすべて二等辺三角形である。 つまり、

である。よって、\( AO=BO=CO \)となり、各頂点から\( O \)までの距離は等しいことが証明できる。

また、3つの二等辺三角形の1つの頂点は1点で交わるのである。

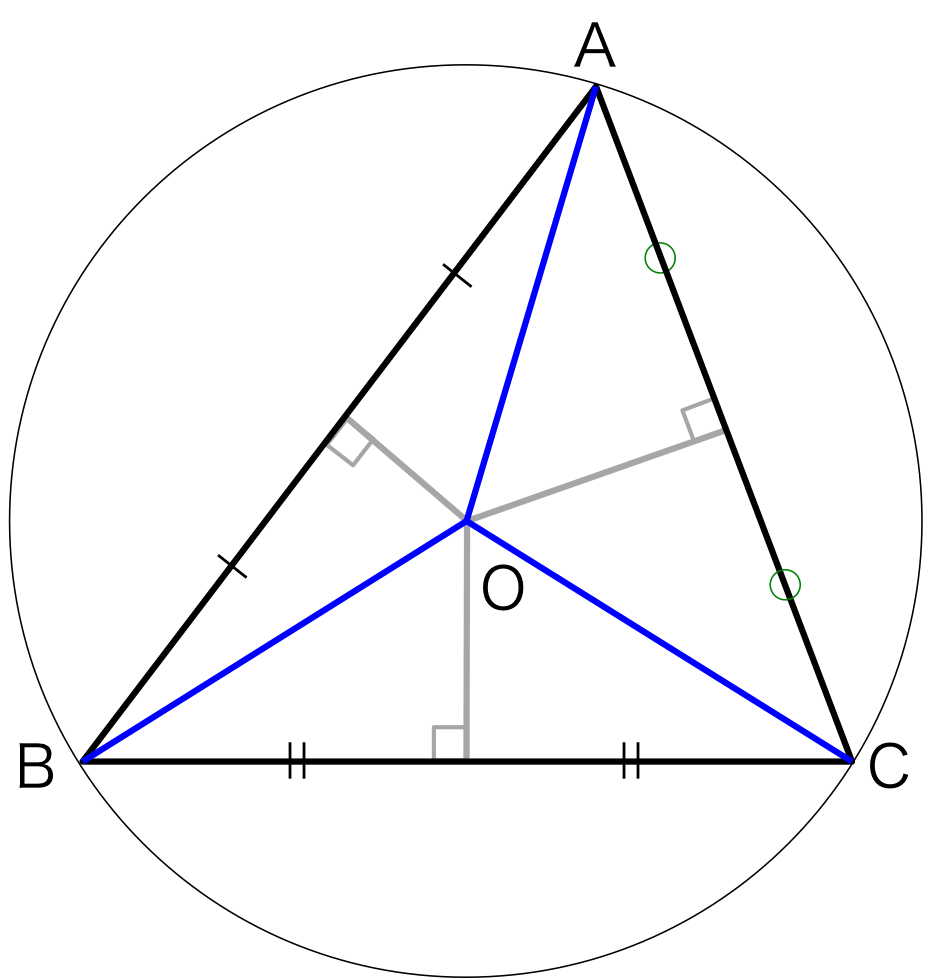
図2.

　このように各辺の垂直二等分線の交わる点のことを外心と呼ぶ。

外心は各頂点からの距離が等しいので、外心を中心として図2のような各頂点を通る円を書くことができる。 この円のことを外接円と呼ぶ。

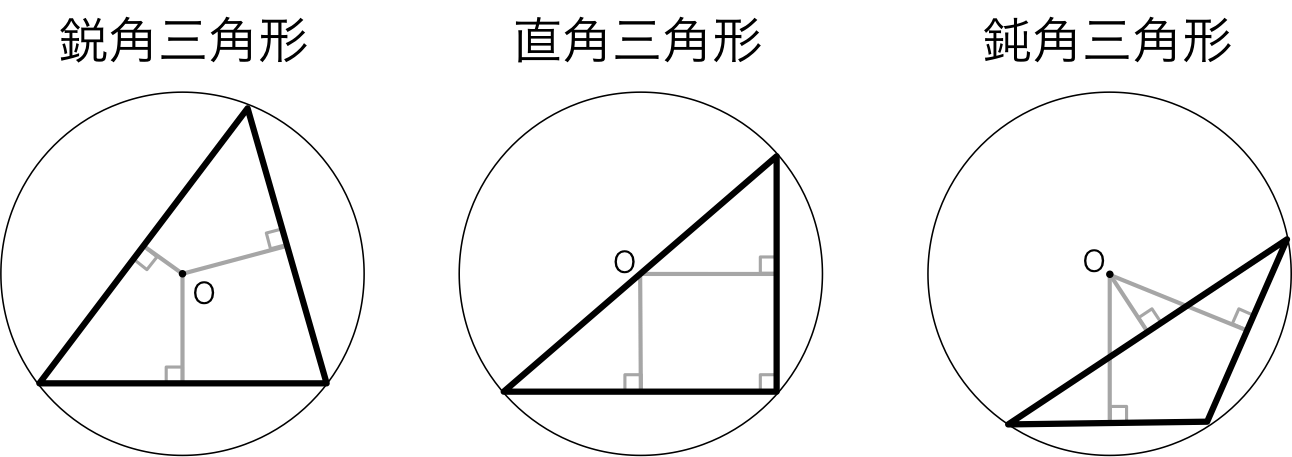
図2.

外接円を書いてみるとわかるが、外心は必ずしも三角形の内部にはこない。

鋭角三角形の場合は内部に外心を持つが、直角三角形の場合は斜辺の中点、鈍角三角形の場合は三角形の外部に外心を持つのである。