三角形の角の二等分線と比
カテゴリー:数学A
三角形の角の二等分線と比には以下の定理がある。
\(\triangle{ABC}\)の\( \angle A\)の二等分線と辺BCとの交点Pは、辺BCをAB:ACに内分する。
\( AB \ne AC \)である\( \triangle{ABC} \)の頂点Aにおける外角の二等分線と辺BCの延長との交点Qは、辺BCをAB:ACに外分する。
ここで、内分と外分は「線分の内分点と外分点」のページを参照して欲しい。 では上の定理について、証明と説明を同時に行っていく。
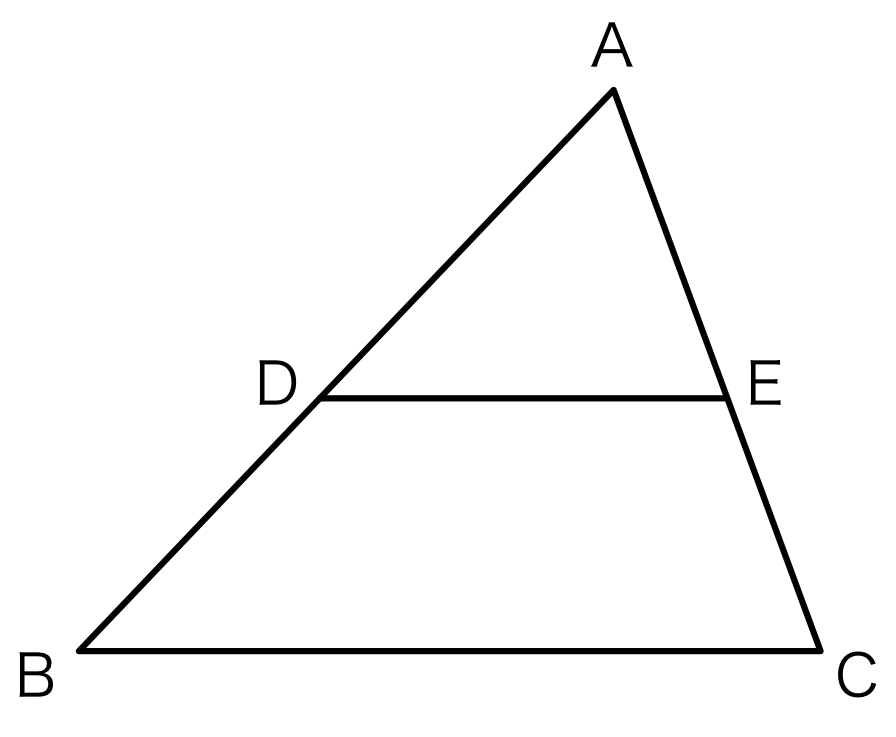
図1.
証明を行う前に、中学校で習った平行な直線と線分の長さとその比に関して、復習して置く必要がある。
図1のように\( \triangle{ABC} \)があり、辺ABと辺AC上に点D, Eがある時、\( PQ \parallel BC \)である時、
AD : AB = AE : AC
AD : DB = AE : EC
AD : AB = DE : BC
が成り立つ。
この時、最後の行の「\( PQ \parallel BC \)であるならばAD : AB = DE : BC」を意味するが、 この逆の「AD : AB = DE : BCならば、\( PQ \parallel BC \)」は成り立たないので注意が必要である。
では、この法則を使って上の定理を証明していこうと思う。
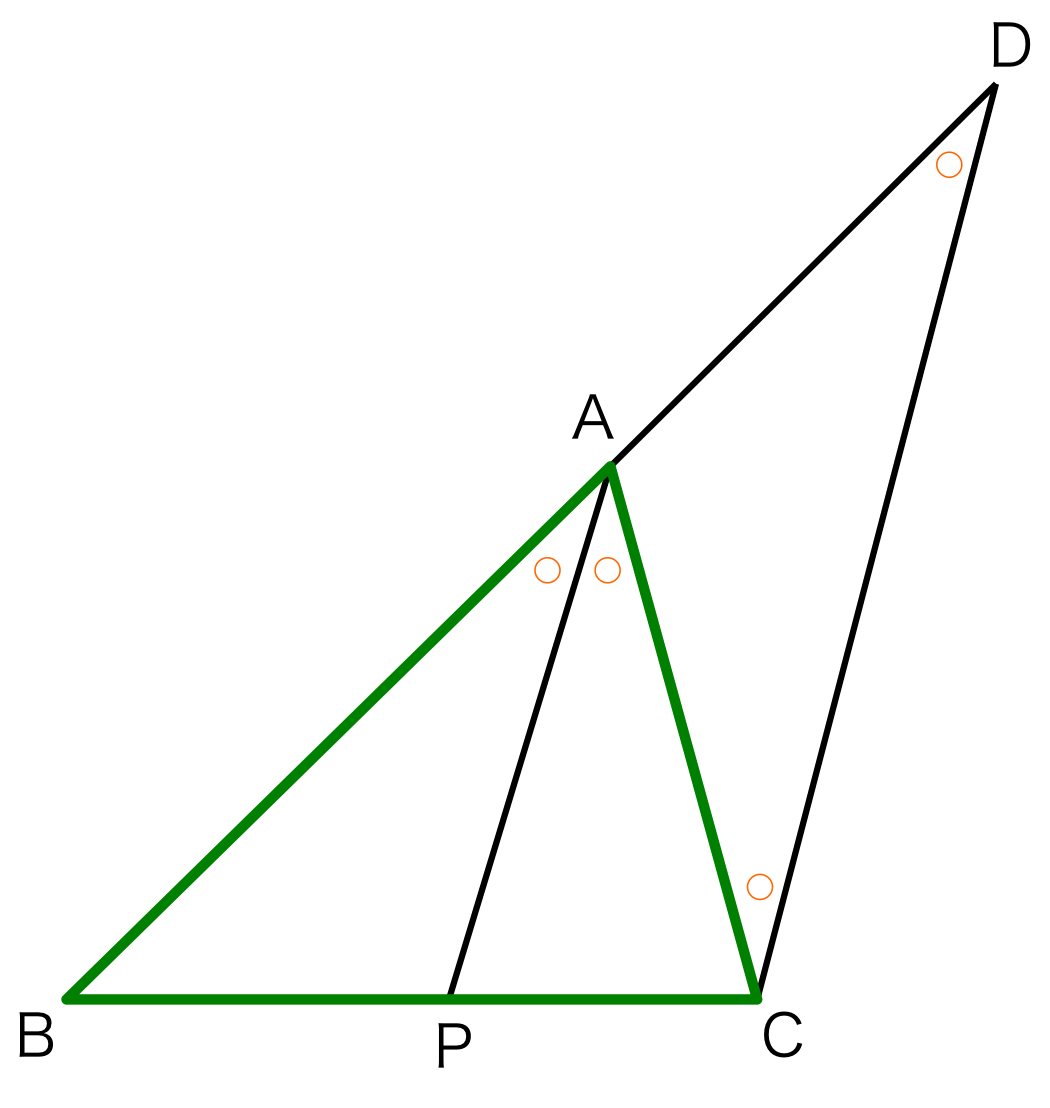
図2.
定理1
図3のような緑の三角形を考える。 \( \angle A\)の二等分線とその二等分線が辺BCと交わる点Pとする。 定理1を証明するためには、
AB : AC = BP : PC
を証明すれば良い。 線分APに平行でCを通る補助線を下記、その補助線と辺ABとの交点をDとする。
\( AP \parallel DC \)であるので、同位角の関係から、
\begin{eqnarray} \angle ADC = \angle BAP \end{eqnarray}
また、錯角の関係から、
\begin{eqnarray} \angle PAC = \angle ACD \end{eqnarray}
である。これらの関係から、\( \angle ADC = \angle ACD \)となり、\( \triangle{ACD} \)は二等辺三角形である。
次に、\( AP \parallel DC \)より、
AB : AD = BP : PC
である。\( \triangle{ACD} \)は二等辺三角形であるので、AD = ACを上の式に代入することができる。 以上より、
AB : AC = BP : PC
を証明することができた。
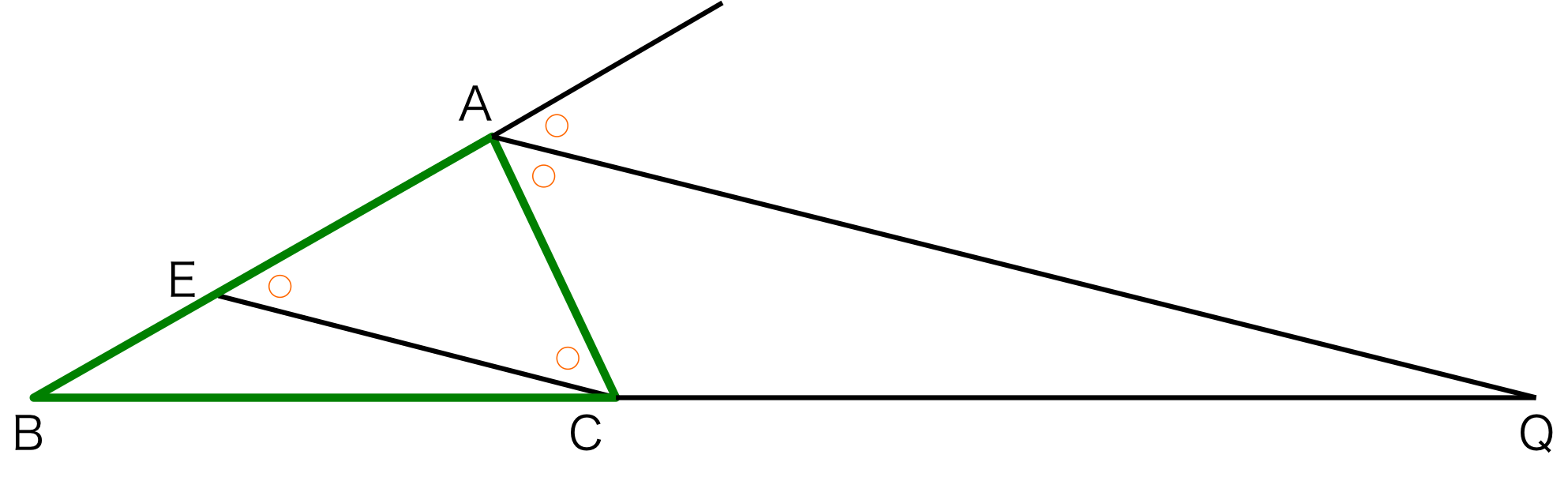
図3.
定理2
定理2を証明するためには、
AB : AC = BQ : CQ
を証明すればよい。では、図3を使って説明する。 点Eは辺AQと平行な点Cを通る直線と辺ABとの交点である。
辺AQは\( \angle A \)の外角の二等分線である。 \( AQ \parallel EC \)であるので、錯角の関係から、
\begin{eqnarray} \angle QAC = \angle ACE \end{eqnarray}
である。次に、\( \angle{EAC} \)は、
\begin{eqnarray} \angle EAC = 180^{\circ} - 2 \angle QAC \end{eqnarray}
で与えられる。
\( \triangle{ACE} \)の内角の和から、
\begin{eqnarray} \angle AEC + \angle EAC + \angle ACE = 180^{\circ} \end{eqnarray}を得る。これを変形すると、
\begin{eqnarray} \angle AEC + 180^{\circ} - 2 \angle QAC + \angle ACE &=& 180^{\circ} \\ \angle AEC - 2 \angle ACE + \angle ACE &=& 0 \\ \angle AEC &=& \angle ACE \\ \end{eqnarray}
を得る。よって、\( \triangle{ACE} \)は二等辺三角形である。つまり、AC = AEである。 また、\( AQ \parallel EC \)であるので、
AB : AE = BQ : CQ
である。AC= AEを使うことで、
AB : AC = BQ : CQ
を証明することができる。