三角形を作るための条件（三角形の成立条件）

カテゴリー：数学A

三角形を成立させる条件について説明する。

三角形には、

2つの辺の長さを足し合わせると残りの1つの辺の長さより長くなる。

また、2の辺の長さを引いた時、残りの1つの辺の長さより短くなる。

という定理がある。

この定理の詳細は三角形の2辺の和と差のページを参考にして欲しい。

この定理を数式にしてみる。

三角形ABCの各辺の長さを\( a,\ b,\ c\)とすると、

\begin{eqnarray} |a-b| < c < a + b \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}

となる。

1つの辺の長さは、2辺の差より大きく、和より小さいということを示しただけである。

この一見単純そうな式は三角形であるための条件を示す重要な式である。

「3cm, 4cm 5cmの直線で三角形は作れるか？」という問題

すると、

\begin{eqnarray} |4-3| < 5 < 4 + 3 \end{eqnarray}

という不等式は成り立つので、この問題の答えは”Yes”となる。

「3cm, 4cm 10cmの直線で三角形は作れるか？」という問題

\begin{eqnarray} |4-3| < 10 < 4 + 3 \end{eqnarray}

という不等式は成り立たないので、3cm, 4cm 10cmという辺の長さでは三角形を作ることができないのである。

これはどういうことなのか、図を使って説明していこうと思う。

式(1)を図1, 2に示す。

3つの辺を表す棒（線分）を黒、赤、青で示す。

そして、黒の棒の両端に青と赤の辺の一方をつける。

この時、赤と青の棒の長さを半径とする円どうしが黒の棒の上以外で重なり合う時、三角形を作ることができる。

文章を読むより図を見た方が明らかだろう。

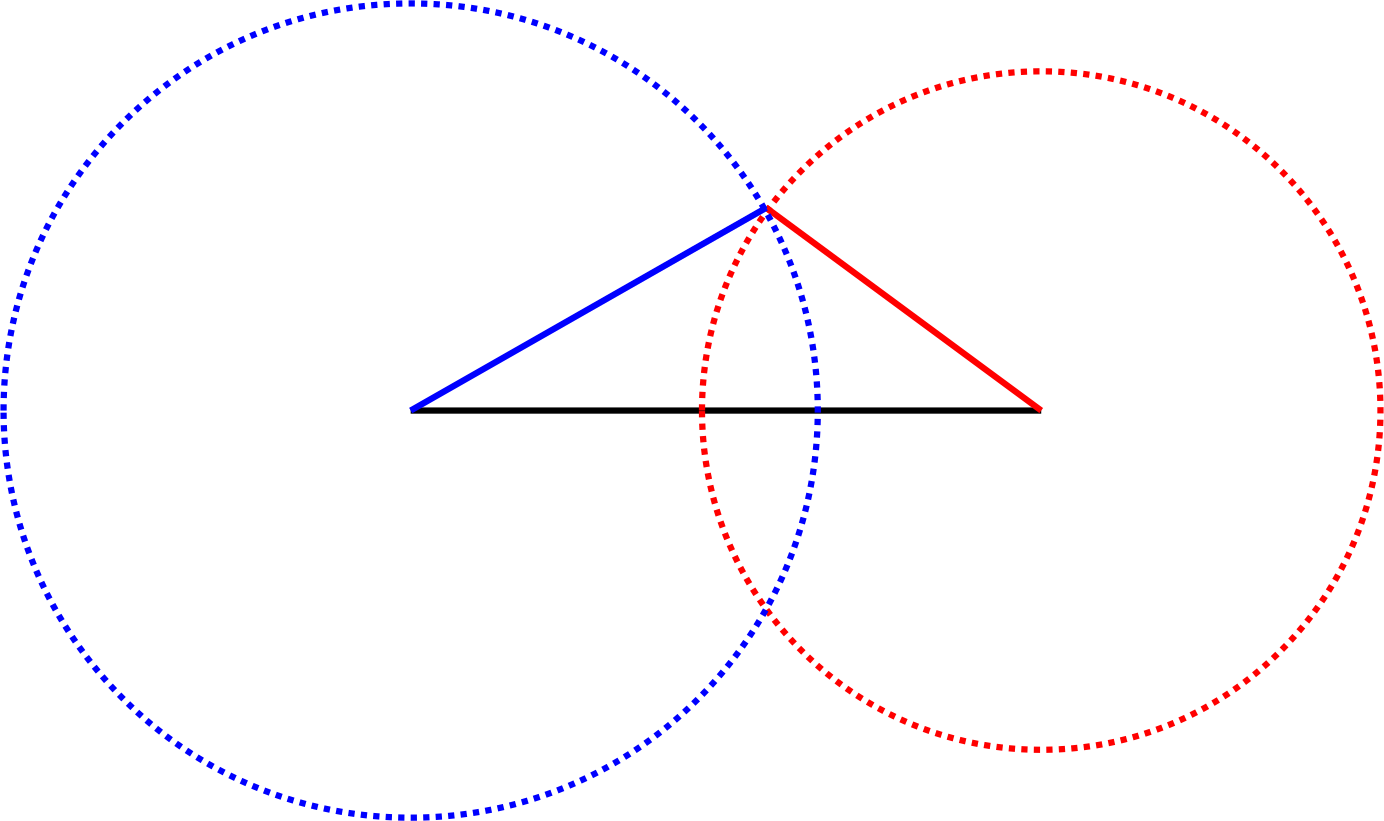
図1.　黒、赤、青の3つの棒を使って三角形が作れる場合

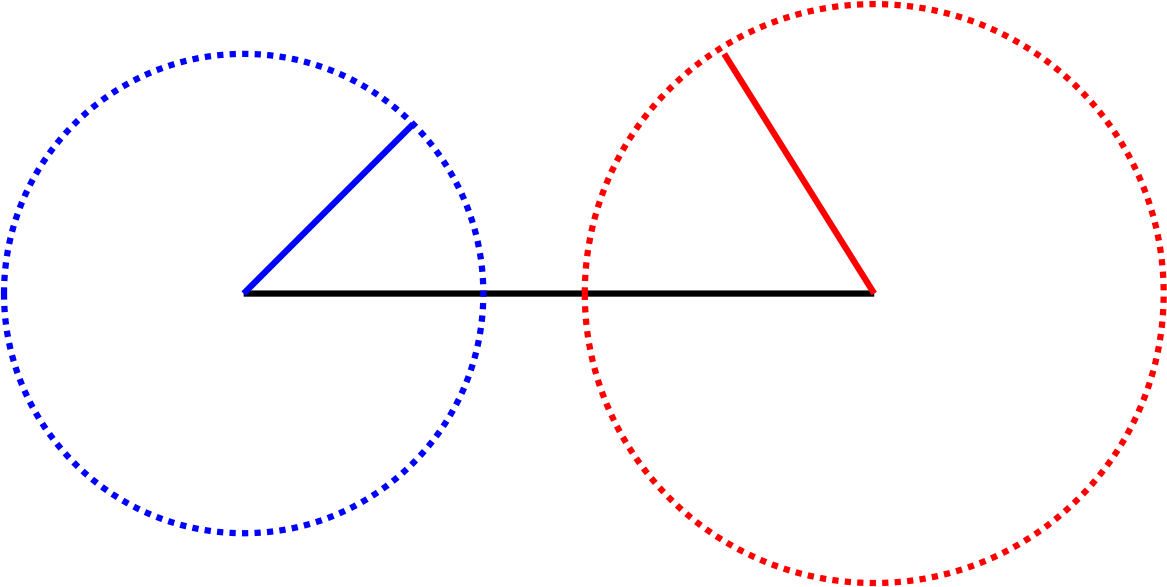
図2.　黒、赤、青の3つの棒を使って三角形が作れない場合

また、三角形を作れない場合は、この円が重なり合うことはない。

この時、3つの棒を使って、それぞれの辺の頂点を繋げ合わせることはできないのである。