三角形の2辺の長さの和と差
カテゴリー:数学A
三角形の3辺の長さについて以下の定理が成り立つ。
三角形の2辺の長さの和は、他の1辺の長さより大きい。
三角形の2辺の長さの差は、他の1辺の長さより小さい。
この定理を簡単に説明しよう。
図1のような三角形があったとする。
この三角形のどの2辺の長さを足し合わせても残りの1辺よりは必ず大きくなる。
または、この三角形のどの2辺の長さを引いても残りの1辺よりは必ず小さくなる。
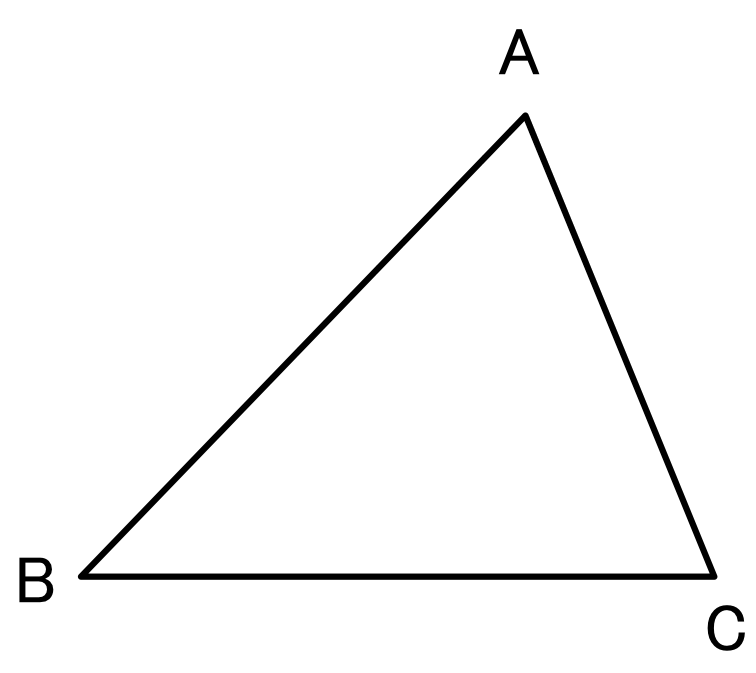
図1.
つまりは、
\begin{align} AB &+ AC > BC \\ AB &+ BC > AC \\ BC &+ AC > AB \end{align}
または、
\begin{align} |AB &- AC| < BC \\ |AB &- BC| < AC \\ |BC &- AC| < AB \end{align}
ということである。
ここで、引き算の際にマイナスになると辺の長さと比べることができなくなるので絶対値を付けた。

図2.
では、図2のように辺ACと同じ長さの辺ADを持つ二等辺三角形を使って、
\begin{eqnarray} AB + AC > BC \ \ \ \ \ \ \ \ (1) \end{eqnarray}
を証明しようと思う。
ここで、DはABの延長線上にあり、三角形DBCも作ることができる。
式(1)の\( AB + AC \)は二等辺三角形の2つの辺の長さは\( AD = AC \)と等しいことを使って、
\begin{eqnarray} AB+AC = AB + AD = BD \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
とすることができる。
つまりは、\( BD > BC \)を証明すれば良いのである。
次に角の大きさを見てみる。
\begin{eqnarray} \angle DCB = \angle BCD + \angle ACB \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
である。
ここで、三角形\( ACD\)は二等辺三角形であるので、\( \angle BCD = \angle ADC \)である。
よって、
\begin{eqnarray} \angle DCB > \angle BDC \ \ \ \ \ \ \ \ \ (4) \end{eqnarray}
の関係が導ける。
ここで、大きい角に対する辺は、小さい角に対する辺より大きいので、
\begin{eqnarray} BD > BC \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
であることが言える。
よって、
\begin{eqnarray} AB + AC > BC \ \ \ \ \ \ \ \ (1) \end{eqnarray}
を証明することができた。
他の辺に対しても、同様に二等辺三角形を作ることで証明することが可能である。
ちなみに、この証明により以下が成り立つことを使って、
\begin{align} AB &+ AC > BC \ \ \ \ \ &(6)\\ AB &+ BC > AC \ \ \ \ \ &(7)\\ BC &+ AC > AB \ \ \ \ \ &(8) \end{align}
2つの辺を引くと残りの1つの辺より短くなるということを証明できる。
式(6), (7)を使って、
\begin{align} AB > BC &- AC \ \ \ \ \ &(9)\\ AB > AC &- BC \ \ \ \ \ &(10)\\ \end{align}
を得る。
つまり、辺ACと辺BCをどの順番で引こうが辺ABよりは大きくなれないのである。
つまり、
\begin{eqnarray} |BC - AC| < AB \end{eqnarray}
を証明することができた。
他の不等式に対しても同様な方法で解くことができる。