三角形の角と辺
カテゴリー:数学A
三角形の角と辺について以下の定理が成り立つ。
1つの三角形において、
大きい辺に向かい合う角は、小さい辺に向かい合う角より大きい。
大きい角に向かい合う辺は、小さい角に向かい合う角より大きい。
これを図にすると以下のようになる。
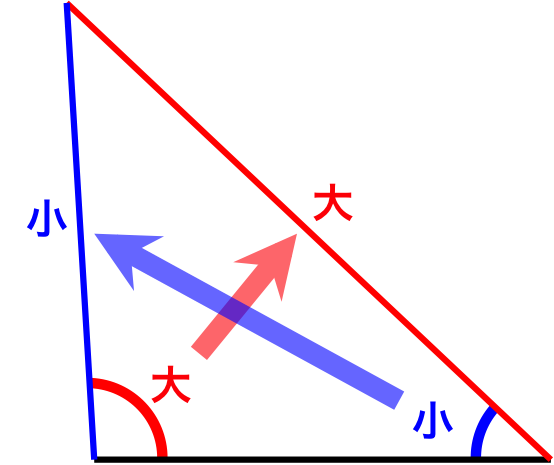
図1.
では、上の定理を証明する。
図2のように三角形の中に二等辺三角形を作るように、辺ABと同じ長さの辺ADを辺AC上に作る。
つまり、\( \triangle{ABD} \)は二等辺三角形であるので、AB = ADである。
よって、辺AC > 辺AB となる。
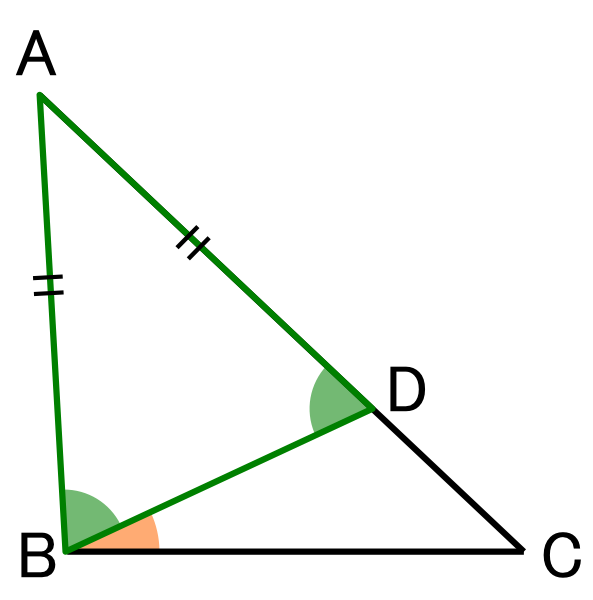
図2.
次に、
\begin{eqnarray} \angle B = \angle ABD + \angle DBC\ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray}
であるので、\( \angle ABD = \angle ADB \)であることを使って、
\begin{eqnarray} \angle B > \angle ADB\ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}
であることが言える。
これは\( \angle DBC\)が負になることはないからである。
また、
\begin{align} \angle BDC &= 180^{\circ} - \angle ADB &\ \ \ \ \ \ \ \ \ \ \ (3)\\ \angle DBC + \angle BDC + \angle C &= 180^{\circ} &(4) \end{align}
であることを使うことで、
\begin{eqnarray} \angle ADB = \angle C + \angle DBC\ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray}
を得る。
これはつまり、
\begin{eqnarray} \angle ADB > \angle C\ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray}
であることを意味している。
式(2)と式(6)より、
\begin{eqnarray} \angle B > \angle C \ \ \ \ \ \ \ \ (7) \end{eqnarray}
となる。
以上より、"辺AC > 辺AB ならば \(\angle B > \angle C \)であることを示すことができた。
また、その逆も真となり、\( \angle B > \angle C \) ならば 辺AC > 辺AB である。
スポンサーリンク