逆・裏・対偶

カテゴリー：数学A

条件\( p \)と条件\(q \)がある時、\( p \Longrightarrow q\)に対して、

\(q \Longrightarrow q\)　を　\( p \Longrightarrow q\)　の　逆（\(p\)と\(q\)を入れ替えただけ）

\( \overline{p} \Longrightarrow \overline{q} \)　を　\( p \Longrightarrow q\)　の　裏 （\(p\)と\(q\)の条件を否定しただけ)

\( \overline{q} \Longrightarrow \overline{p} \)　を　\( p \Longrightarrow q\)　の　対偶　（命題を逆にして裏にしたもの）

である。これを図示したものが図1である。

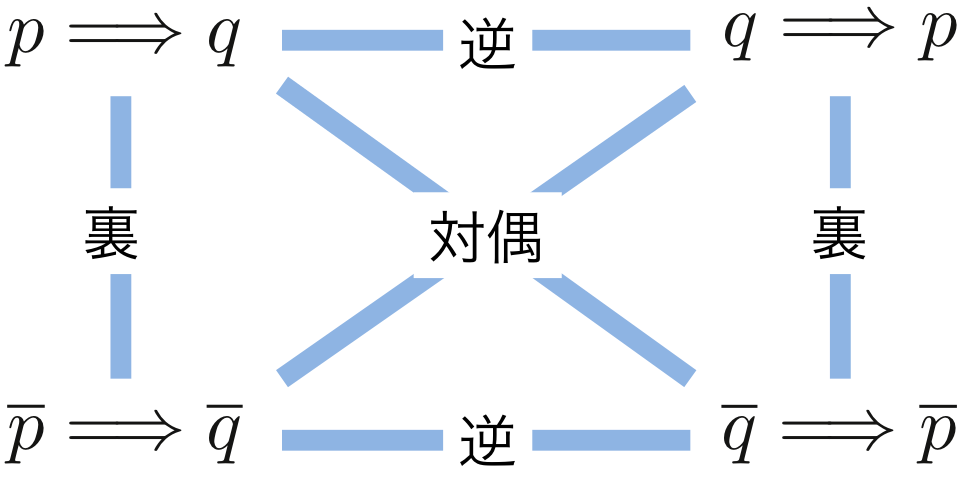
図1.

文字式だけだとわかりにくいので、実際の例題を取り扱ってみる。

「\(x\)を実数とするとき、\(x=1 \Longrightarrow x^2=1\)」の逆、裏、対偶を求めよ。

逆は、矢印の両端を入れ替える。

裏は、矢印の両端を否定する。

そして、対偶は裏の逆を取る。

　逆は　\( x^2 = 1 \Longrightarrow x=1\)

　裏は　\( x \ne 1 \Longrightarrow x^2 \ne 1 \)

　対偶は　\( x^2 \ne 1 \Longrightarrow x \ne 1 \)

である。ここで、それぞれの真偽を見ていこうと思う。

まず、\(x=1 \Longrightarrow x^2=1\)は真である。

逆はどうだろうか？

しかし逆、\( x^2 = 1 \Longrightarrow x=1\)は反例\(x=-1\)があるので偽である。

つまり、

真である命題の逆は、必ずしも真ではない。
（真の可能性も偽の可能性もある）

ということが言える。

裏はどうだろうか？

裏は\( x \ne 1 \Longrightarrow x^2 \ne 1 \)で、同様に反例\( x=-1 \)があるので、命題が真であってもその裏が必ずしも真とは限らないのである。

対偶はどうだろうか？

対偶は\( x^2 \ne 1 \Longrightarrow x \ne 1 \)である。

これは反例が見つからない。

つまり、真である。

では、真である命題の対偶は常に真になるのか調査してみる。

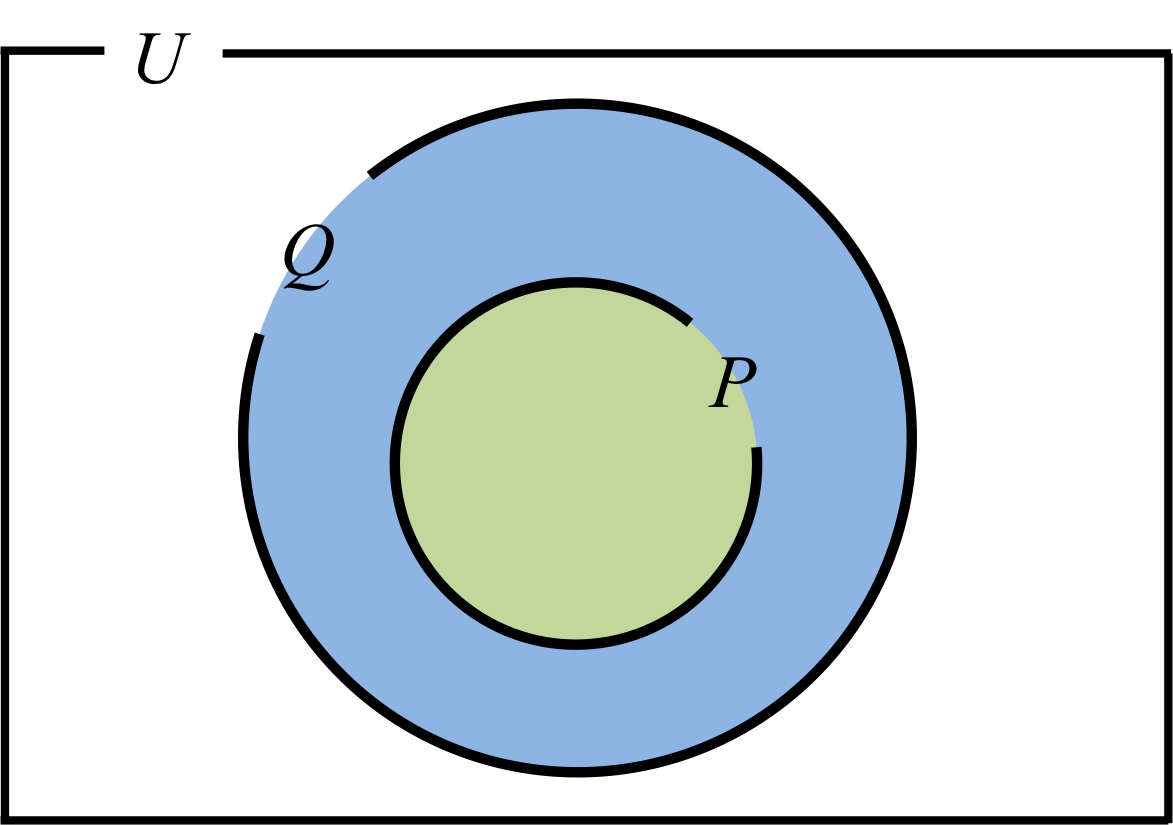
図2.

もう一度、命題が真であるということはどういうことか確認する。

条件\( p \)を満たす集合を\( P \)、条件\( q \)を満たす集合を\( Q \)とする。

その時、\( p \Longrightarrow q \)が真であるということは\( P \)は\( Q \)の部分集合であるということである。

よって、対偶\( \overline{q} \Longrightarrow \overline{p} \)が真であるということは\( \overline{Q} \) は\( \overline{P} \)の部分集合であれば良い。

図2でそれを確認すると、\( P \subset Q\)ということは\( \overline{Q} \subset \overline{P} \)であることと同値であることがわかる。

つまり、

\( P \subset Q \Longleftrightarrow \overline{Q} \subset \overline{P} \)

である。つまり、

　命題\( p \Longrightarrow q \)とその対偶\( \overline{q} \Longrightarrow \overline{p} \)の真偽は一致する。
よって命題を証明する場合は、その対偶を証明しても良い。

ということが言えるのである。