必要条件・十分条件・必要十分条件

カテゴリー：数学A

2つの条件、\(p\)、\(q\)に対して、「\(p\)ならば\(q\)（\( p \Longrightarrow q\) ）」が真であるとき、

\(q\)は\(p\)であるための必要条件である。

\(p\)は\(q\)であるための十分条件である。

という。また、\( q \Longrightarrow p\)も同時に成り立つ時、

\(p\)は\(q\)であるための必要十分条件である。

\(q\)は\(p\)であるための必要十分条件である。

という。このとき、\( p \)と\( q\)は同値であるともいう。

必要条件と十分条件の関係を図1に示す。 文字で示しても分かりにくいので具体的な例を挙げていこうと思う。

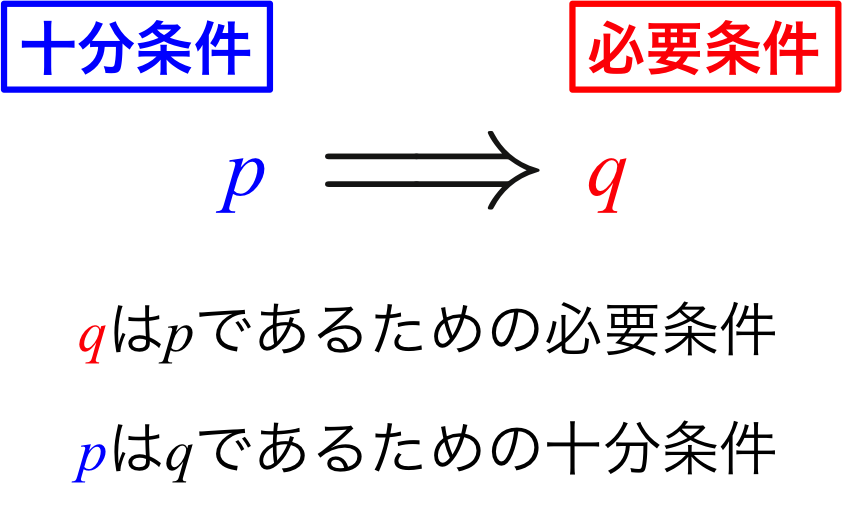
図1.

「パンダである」という条件と「動物である」という条件がある時、

　パンダである　ならば　動物である

は真だろうか？ パンダの中に動物でないパンダはいないので、これは真である。 この時、

動物であることはパンダであることの必要条件である。

パンダであることは動物であることの十分条件である。

と言える。では、「パンダである」ということと「動物である」ということの関係はどのような関係になっているのであろうか？

その関係をベン図で示したものが図2である。

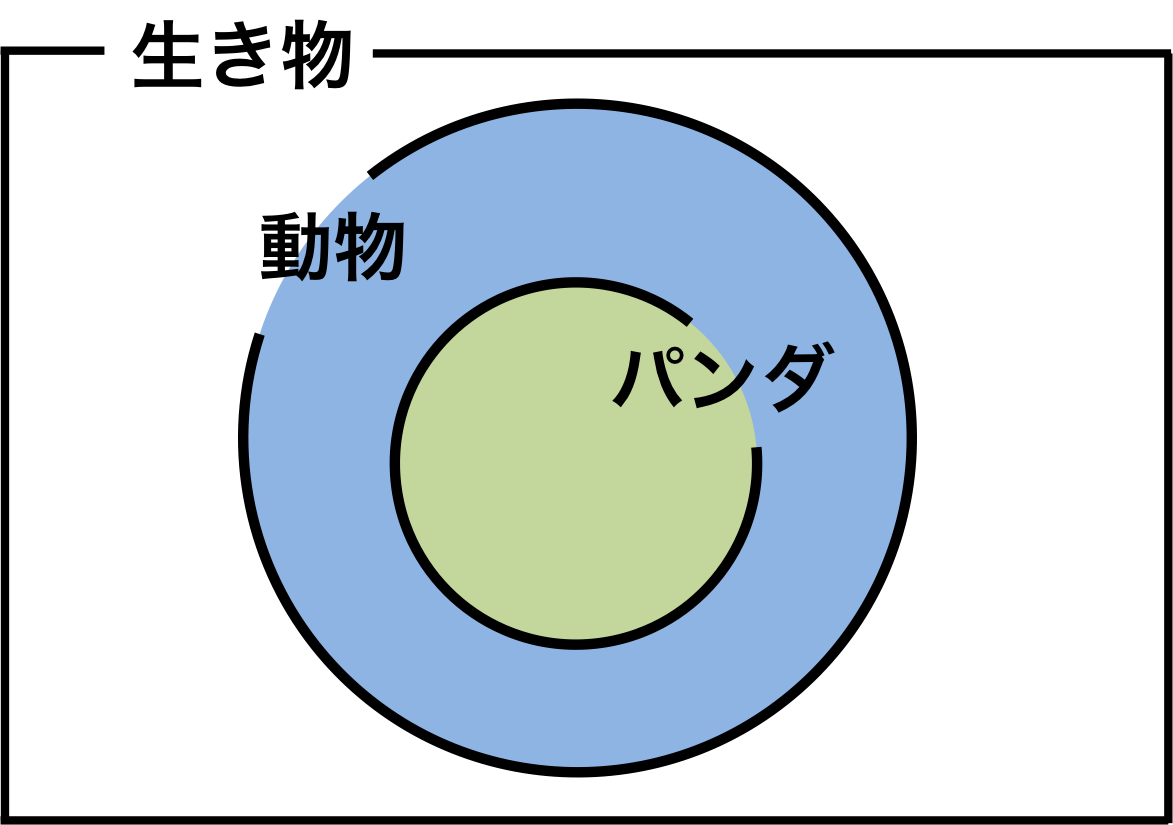
図2. 動物とパンダの関係

「生き物である」という全体集合の中に「動物である」という集合と「パンダである」という集合がある。

もちろん「パンダである」というのは「動物である」という集合の部分集合である。

つまり、主語で表される集合がその後ろに示される集合の部分集合である場合は必要条件であると言え、 後ろに示される集合が主語で表される集合の部分集合である場合は十分条件であると言える。

相当砕けた言い方で言うと、「主語が大きい方が必要条件、小さい方が十分条件」である。

図2の「パンダである」という集合は「動物である」という集合からはみ出してはいけない。

では、必要十分条件はどのように表されるのだろうか？

今度は条件を変えて、「パンダである」という条件と「主に中国に生息し白と黒の毛に覆われたクマ科の動物」という条件があったとする。

このベン図を描いてみると、

図3.

となる。パンダにはレッサーパンダも含まれるじゃんというようなツッコミは無視するとして、「主に中国に生息し白と黒の毛に覆われたクマ科の動物」はパンダしか該当しない。

反対に野生のすべてのパンダは「主に中国に生息し白と黒の毛に覆われたクマ科の動物」である。

このように2つの条件で表される集合が全く一致する時、両者は必要十分条件、または同値であると言える。

では、次のページでテストや試験で出題される必要条件、十分条件、必要十分条件の問題の解き方を説明しようと思う。