条件の否定

カテゴリー：数学A

条件\( p\)に対して、「\(p\)でない」という条件を条件\(p\)の否定という。

例えば、整数\(x\)に対して「\(x\)は偶数である」であるという条件の否定は「\(x\)は奇数である」ということである。

この時、条件\(p\)の否定は\( \overline{p}\)で表される。

これは、補集合や余事象を表す場合と同じである。

では、少しだけ条件の否定の例を示す。これでおおよその感じは掴めると思う。

\(x\)を実数とする。

(A)「\(x=7\)」の否定は「\(x \ne 7\)」

(B)「\(x<3\)」の否定は「\(x \geqq 3\)」

　では条件の否定によってどのようなことが説明できるか見ていこうと思う。

全体集合を\(U\)として、条件\(p\)と条件\(q\)を満たす集合をそれぞれ\(P\)と\(Q\)とする。

すると、\( P\)と\(Q\)の間には図1のような関係が成り立つ。

図1.

つまり、「条件の否定」の場合には「補集合」、「かつ」の場合には「共通部分」、「または」の場合には「和集合」で表されることがわかる。

このことから、集合に関してはド・モルガンの法則が成り立つので、 条件\(p\)と条件\(q\)に関しても以下のことが成り立つ。

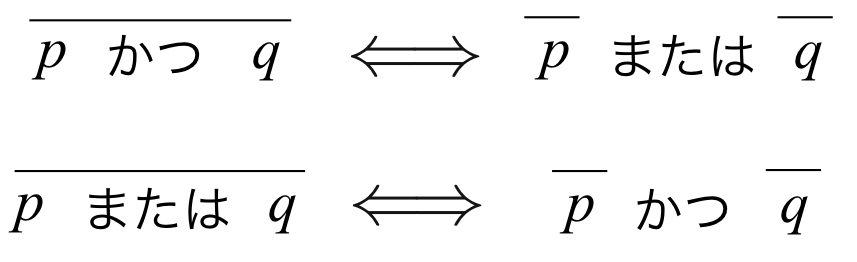
バーは否定を表すことを思い出しておこう。この法則の簡単な例は、

　\(x\)と\(y\)を実数とする。

　(A) 「\(x=1\) かつ \(y=1\)」 の否定は 「\(x\ne 1\) または \(y\ne 1\)」

　(B) 「\(x>0\) または \(y>0\)」 の否定は 「\(x\leqq 0\) かつ \(y\leqq 0\)」

である。