条件と集合
カテゴリー:数学A
例えば文字\( x\)を含んだ文や式において、その文字の取る値を変化させると、真偽が変わるのもがある。
例えば、「\(x\)は偶数である」という文があった場合、\(x\)=2であれば、命題は真であるが、\( x=3 \)の時は偽となる。
このように文字\( x\)を含んだ文を、「\(x\)に関する条件」と呼ぶ。
条件を考える場合は、その条件の対象となるものの全体の集合を初めに定義しておく必要がある。
例えば、「\(x\)は実数とする」や「\(x\)は正の整数とする」と言った具合である。<
こういう全体の集合を全体集合という。
条件を設定する前には必ず全体集合を定義しなければならない。
別ページで説明した命題は基本的に、2つの条件\(p,\ q\)を組み合わせて「\(p\)ならば\(q\)」と言うように表される場合がほとんどである。
例えば、「\(x\)を実数とするとき、\(-2 < x < 2\)ならば、\(x<5\)である」と言った形で表される。
このように命題「\(p\)ならば\(q\)」は\( p \Longrightarrow q \)と書くことができて、\( p\)をこの命題の仮定、 \(q\)をこの命題の結論と呼ぶ。
また、先ほどの命題の\(p\)と\(q\)を入れ替えて、「\(q\)ならば\(p\)」も同時に成り立つ時、「\(p\)ならば\(q\) かつ \(q\)ならば\(p\)」と表され、 \( p \Longleftrightarrow q\)と書くことができる。
全体集合\( U \)を実数全体とする時、
という命題は真である。この命題の仮定、「\( -2 < x < 2\)」と、結論「\(x<5\)」に対して以下の2つの集合を考える。
\(P = \) { \(x | -2 < x < 2\), \(x\)は実数 }
\(Q = \) { \(x | x < 5 \), \(x\)は実数 }
この2つの集合を図で表すと図1のようになる。
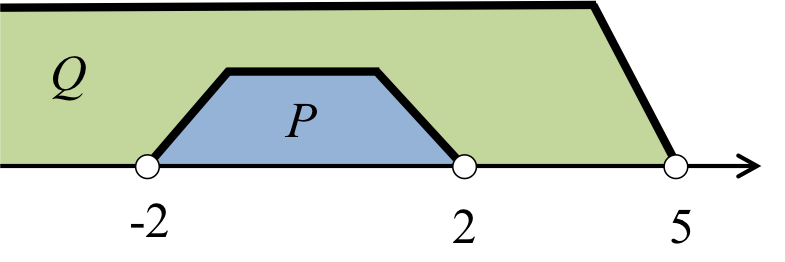
図1.
この図はよく命題の真偽を判定するために用いられる図である。白丸はその数を含まないことを表している。
つまり、白丸は、「\( < \)」や「\( >\)」に相当する。その数を含む場合である、「\( \geqq\)」や「\( \leqq \)」は黒丸で表される。
この時、\(Q\)の一部が\( P\)となっていることがわかる。つまり、\( P \)は\(Q\)の部分集合であることがわかる。
また、\( P \)と\( Q\)の関係をベン図で書くと図2のようになる。
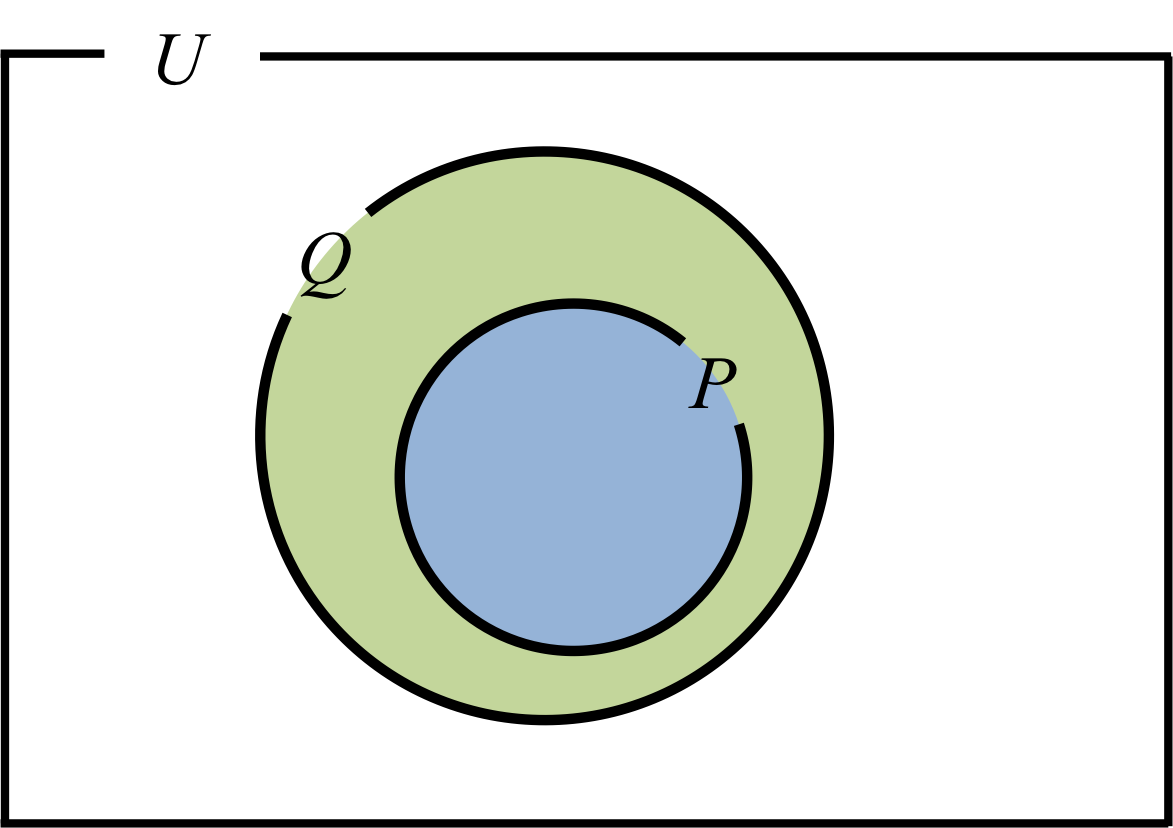
図2.
一般に、全体集合を\( U\)とする命題「\(p\ \Longrightarrow q\)」において、 \( p \)の条件を満たす集合を\( P \)、\( q\)の条件を満たす集合を\( q \)とした時、 もしこの命題が真であるならば、\( P \)は\( Q\)の部分集合となる。
つまり、命題が真ならば、\( P \subset Q\)であると言える。
これは反対のことも言えて、\( P \subset Q\)であるならば、命題「\(p\ \Longrightarrow q\)」は真ということもできる。
また、命題が「\( p \Longleftrightarrow q\)」である時、集合\( P \)と集合\( Q\)は同じになるので、\(P=Q \)である。
以上のことをまとめると、
\(p \Longrightarrow q\)が真であるならば、\( P \subset Q\)である。
\(p \Longleftrightarrow q\)が真であるならば、\( P = Q \)である。
であることが言える。
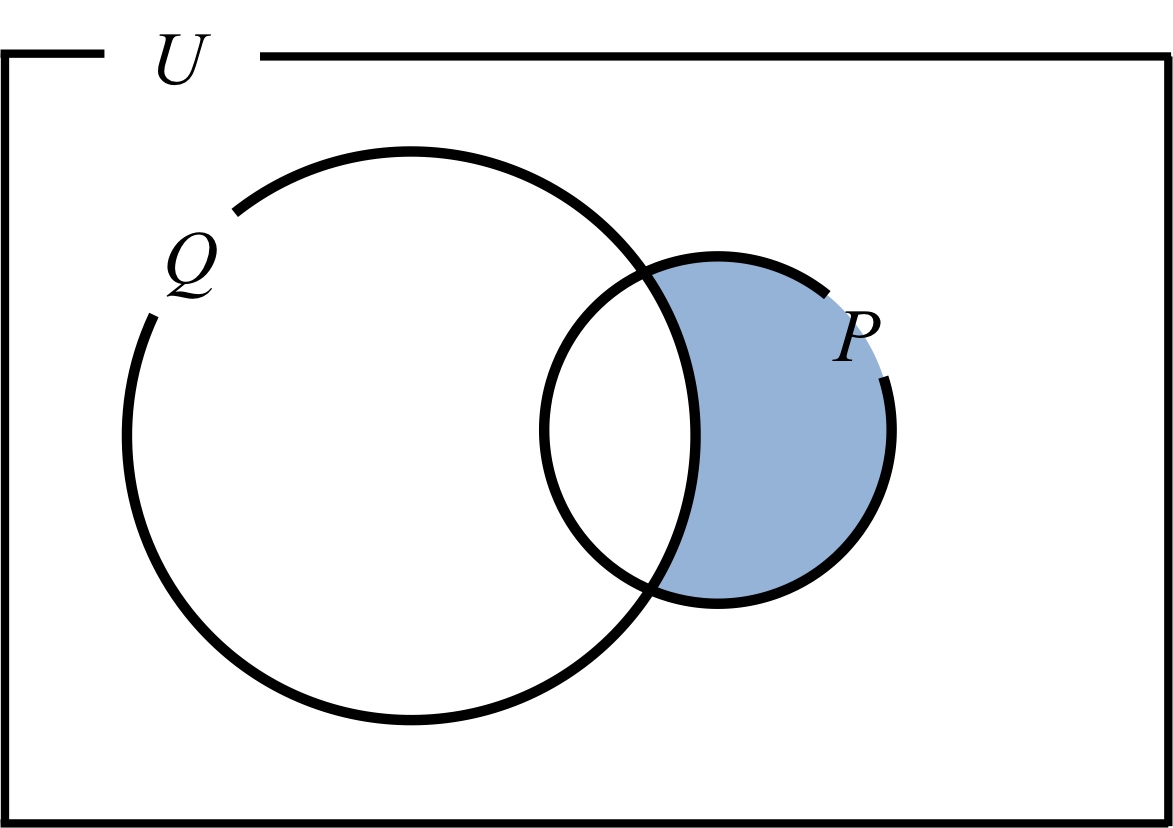
図3.
もし、命題\( p \Longrightarrow q \)が偽である時、\( P \subset Q \)が成り立たない時である。
こういう場合は図3のような状況となる。
つまり、図3で示された色を付けられた領域である\( P \cap \overline{Q}\)が存在するということである。
このように、仮定\( p \)は満たすが、結論\( q\)は満たさない要素のことを、命題の反例と呼ぶ。
もし、命題が偽であることを示したければ、反例を1つ上げれば良い。 例えば、
「\(n\)を自然数とする。\(n\)が3の倍数である \( \Longrightarrow\) \(n\)は6の倍数である」
という命題が真か偽か知りたいとする。
この時、\( n=9 \)は3の倍数ではあるが、6の倍数ではないので、\(n=9\)が反例となり、この命題は偽であることが証明できるのである。