余事象の確率

カテゴリー：数学A

全事象を\( U \)とする。

その中の事象\( A \)に対して、\( A \)が起こらないと言う事象を\(A\)の余事象と呼び、\( \overline{A} \)と表す。

例えば、さいころ1個を振るという試行を行なった時、「奇数の目が出る」という事象を\( A \)とした時、奇数の目、 すなわち1, 3, 5以外の目が出る場合が\( \overline{A} \)に相当するのである。

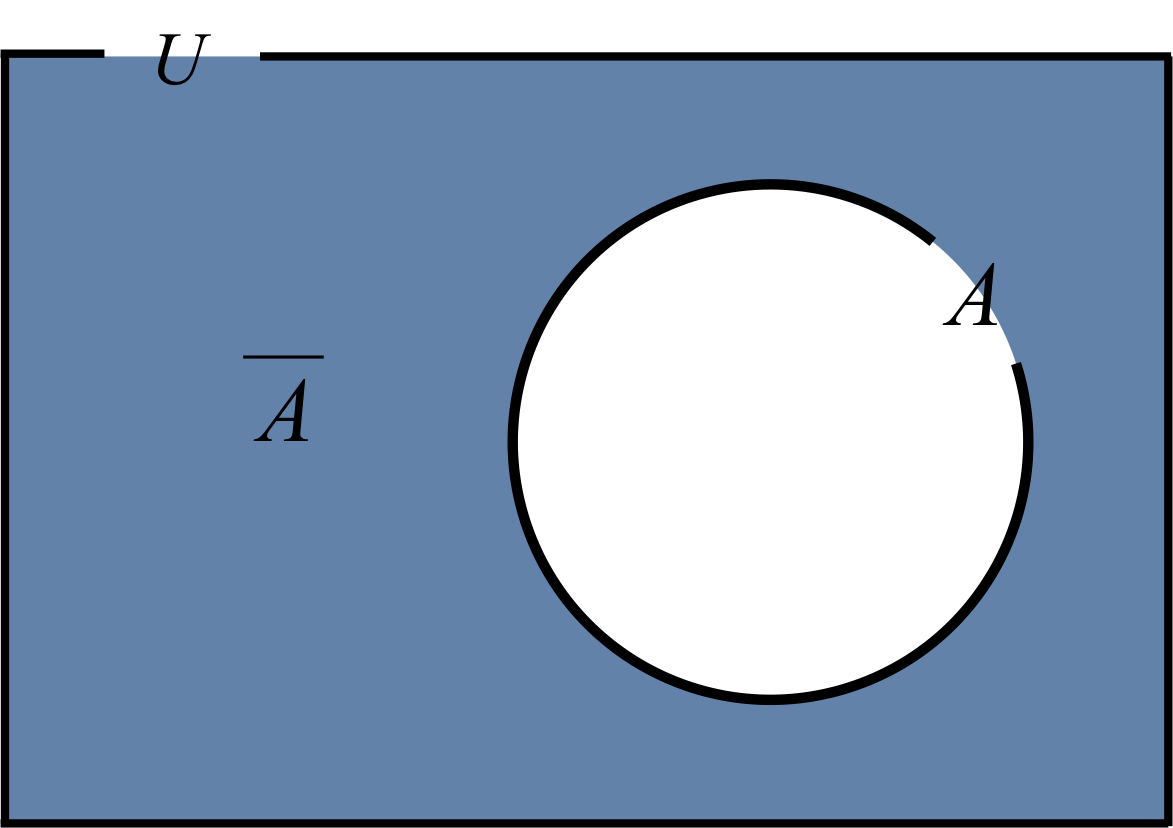
図1. 余事象

ちなみに、\( A \cap \overline{A} = \varnothing \)であるので、\( A \)と\( \overline{A} \)は違いに排反である。

また、\( A \)が起こらない場合は必ず\( \overline{A} \)が起こる。

つまり、以下の関係が導ける。

この式の意味は簡単である。

\( A \)が起きる確率は\( P(A) \)である。

\( A \)が起きない確率は\( \overline{A} \)が起きる確率であるので、\( P(\overline{A}) \)は1から\( A \)が起きる確率\( P(A) \)を引いてやれば良いのである。