和事象の確率
カテゴリー:数学A
ある全事象\( U\)、ある事象\(A\)、\(B\)がある場合を考える。
事象\(A\)と事象\( B \)が起こる確率\(P(A),\ P(B)\)はそれぞれ、
\begin{align} P(A) &= \frac{n(A)}{n(U)} &(1) \\ \\ P(B) &= \frac{n(B)}{n(U)} &(2) \end{align}
と表される。では、事象\(A\)と事象\(B\)の和事象\( A \cup B \)が起こる確率\( P(A \cup B) \)はどのように表されるだろう。
もし、図1のように事象\(A\)と事象\(B\)が互いに共通部分を持たない場合は、簡単に
\begin{eqnarray} P(A \cup B) = P(A) + P(B) \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray}
であることがわかるだろう。
これを確率の加法定理と言う。
わかりやすい例をあげると、さいころを1回振るという試行を行い、事象\(A\)を「3の目が出る」とし、事象\(B\)を「5の目が出る」としたとする。
この時の和事象\(A\cup B\)は「3の目か5の目が出る」という事象となる。

図1. 互いに排反な事象\(A\)と事象\(B\)
両者は共通部分を持たない(1回さいころを振って3と5の目が出ることはありえない)ので、\(A\)と\(B\)が起こる確率\(P(A)\)、\(P(B)\)は、
\begin{eqnarray} P(A) &=& \frac{1}{6} \\ P(B) &=& \frac{1}{6} \end{eqnarray}
である。よって、\( A \)と\( B\)の和事象\( A \cup B\)が起こる確率\( P(A\cup B) \)は、式(3)を使って、
\begin{eqnarray} P( A \cup B ) = \frac{1}{6} + \frac{1}{6} = \frac{1}{3} \end{eqnarray}
と導けるのである。
このように、事象\( A \)と事象\( B\)が共通部分を持たないとき、「互いに排反である」 または、「事象\( A \)と事象\( B\)は排反事象である」と言う。
では次に、事象\( A \)と事象\( B\)が共通部分を持っている場合を考える。
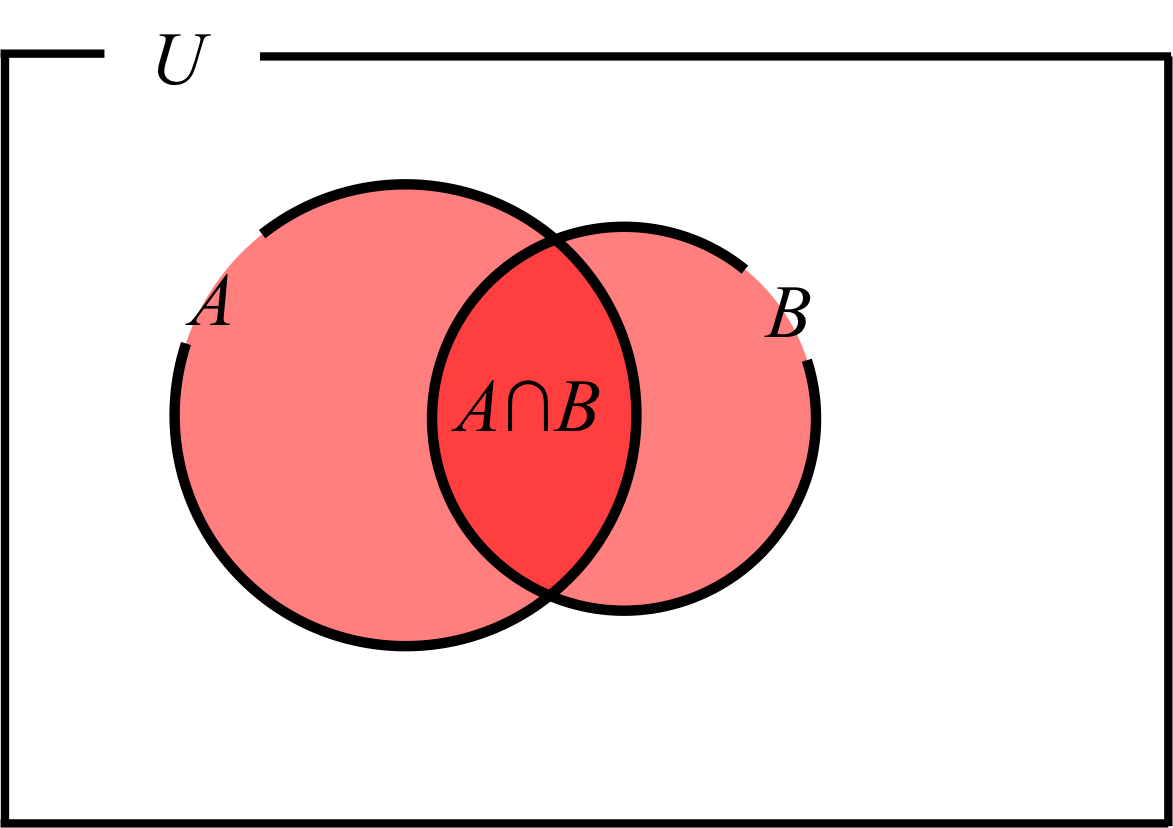
図2. 共通部分を持つ事象\(A\)と事象\(B\)
事象\( A \)と事象\( B\)が共通部分を持っている場合は、図2のようになる。
つまり、和集合の要素数が重要になっている。
では簡単な例を使って考えてみる。
さいころを1回振る時、偶数が出るという事象を\(A\)、3以下の目が出るという事象を\( B \)とすると、
\(B\) = {1, 2, 3}
であることがわかる。この時、共通部分\( A \cap B\)は、
\begin{eqnarray} A \cap B = \{2\} \end{eqnarray}
である。\( A \cap B\)の要素は{2}のみで、要素数は1である。
よって、1つだけ被っている。
この被っている数を\(A\)の要素数と\(B\)の要素数から引いてやれば、和事象の要素数が得られる。
このことから、和事象\( A \cup B \)の要素数\( n(A \cup B) \)は、以下のように表される。
\begin{eqnarray} n(A \cup B) = n(A) + n(B) - n(A \cap B) \end{eqnarray}
和事象の確率は上の式全体を全事象\( U\)の要素数で割ればいいので、和事象の確率は
\begin{eqnarray} P(A \cup B) = P(A) + P(B) - P(A \cap B) \end{eqnarray}
であることを導ける。
和集合の確率は和集合の要素数を全体の要素数で割ると求めることができる。