排反事象

カテゴリー：数学A

1個のさいころを1回振る時、「偶数の目が出る」という事象を\(A\)、「3の目が出る」という事象を\(B\)とすると、

\begin{eqnarray} A &=& \{2,\ 4,\ 6\} \\ B &=& \{3\} \end{eqnarray}

となる。1個のさいころを1回振る事象を全体\( U\)とするとき、事象\(A\)、事象\(B\)の関係をベン図に示すと図1となる。

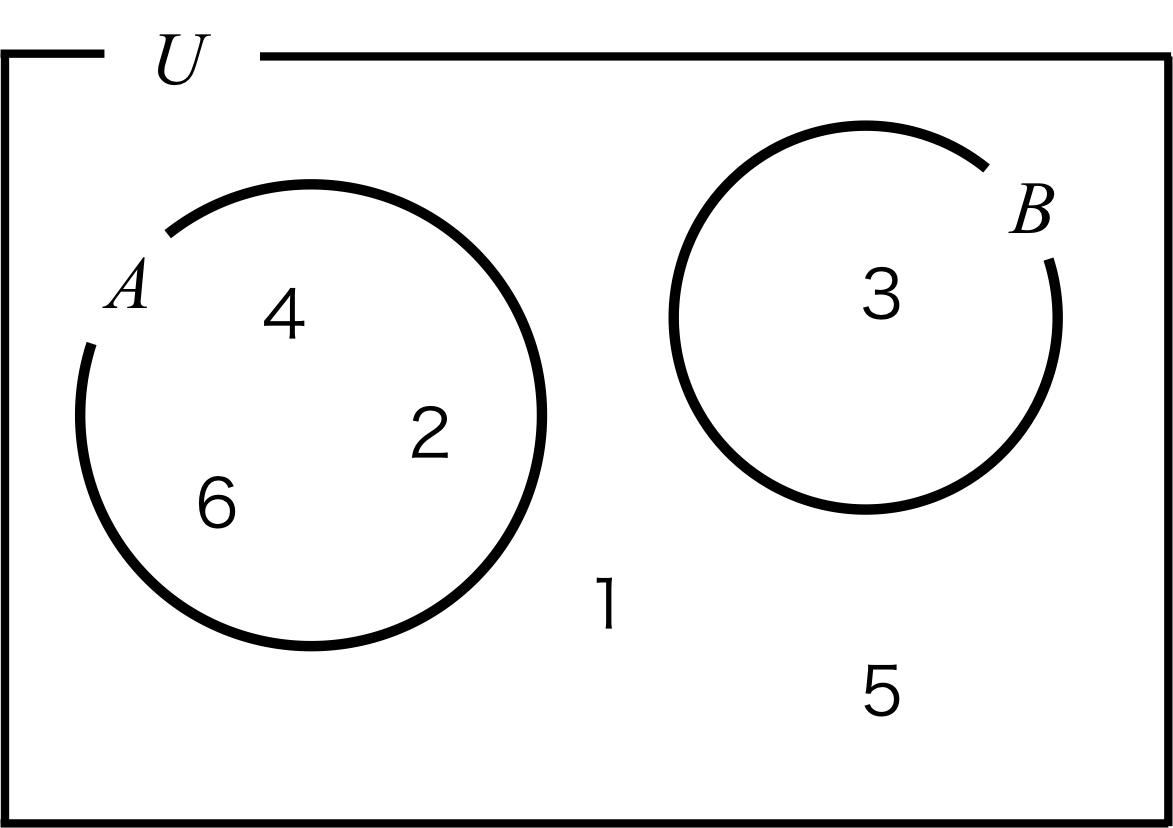
図1. 排反事象

ベン図を見てわかるように、さいころを1回振る時に偶数が出て、3の目が出るということはありえない。

よって、\(A\)と\(B\)は決して同時に起こることはないのである。つまり、

\begin{eqnarray} A \cap B = \varnothing \end{eqnarray}

なのである。このように事象\(A\)、事象\(B\)が決して同時に起こることがない時、 2つの事象は互いに排反（はいはん）であるという。

または、2つの事象は互いに排反事象であると言う。