積事象と和事象

カテゴリー：数学A

さいころを1回振る時、偶数が出るという事象を\(A\)、3以下の目が出るという事象を\( B \)とすると、

となる。

さいころを一回振る事象を全体事象\(U\)として、事象\( A \)と事象\(B\)の関係を図に示すと、図1のようになる。

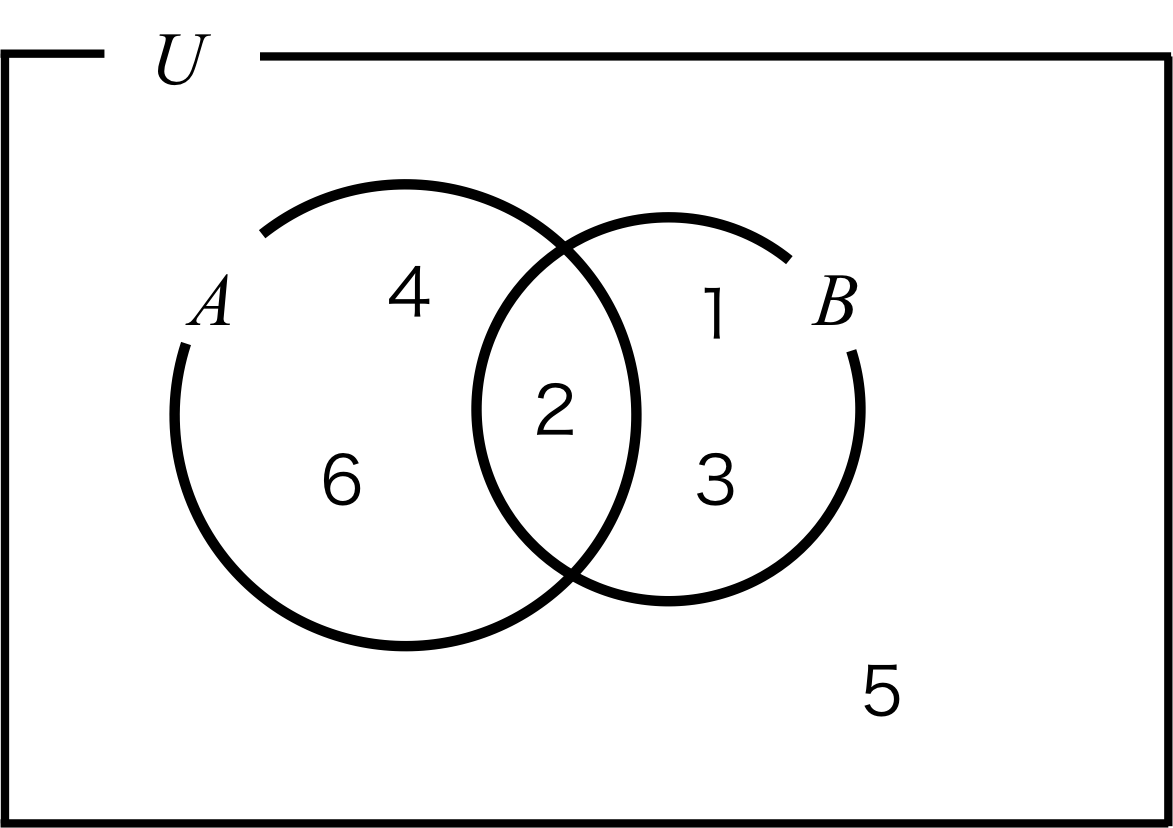
図1. さいころを1回振る時に出る目の全体事象\( U\)、偶数が出る事象\( A \)、3以下の目が出る事象\( B\)

このように集合や事象などの関係を視覚的に表した図をベン図と言う。

ベン図はベン図を考案したイギリスの数学者ジョン・ベンにちなんでいる。

事象\(A\)と事象\(B\)の関係がわかったところで、

と言う事象は、\(A\)と\( B\)の共通部分である、\(A \cap B\)で、{2}であることがわかる。または、

と言う事象は、\(A\)と\( B\)の和集合である、\(A \cup B\)で、{1, 2, 3, 4, 6}であることがわかる。

図2. 積事象(左)と和事象（右）

このように、2つの事象\(A\)、\(B\)がある時、「事象\(A\)が起こり、かつ事象\(B\)が起こる」 という事象を\(A\)と\(B\)の積事象といい、\( A \cap B\)で表される。

また、「事象\(A\)、または事象\(B\)が起こる」という事象を\(A\)と\(B\)の和事象といい、 \( A \cup B\)で表される。

事象を取り扱う場合でも、積事象と和事象は、共通部分\(A\cap B\)と、和集合\( A\cup B\)と同じように表現するのである。 （意味も同じである）