重複順列

カテゴリー：数学A

重複順列とは、同じものを繰り返し取ってもよいという条件つきの場合にできる順列のことである。

つまり、異なるものを選び取る順列に対して、重複順列は同じものを選び取っていいということである。

1, 2, 3, 4, 5の数字を使って、4桁の整数を作る。この時作られる正の整数は何通りあるだろう？

この例題の説明をしていこうと思う。

例題を図にすると、図1のように、千の位、百の位、十の位、一の位に1から5の数字を選んで行くことになる。

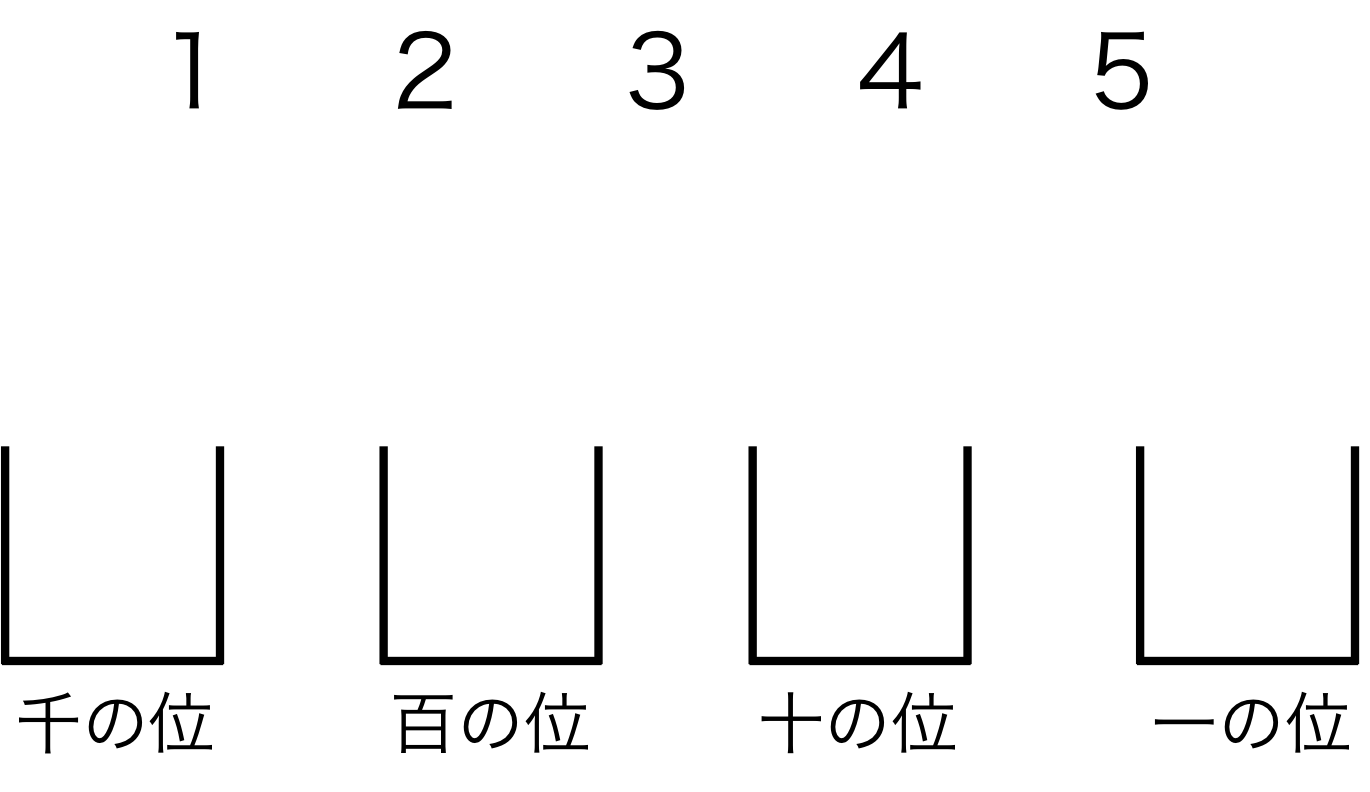
図1.

この場合、千の位には1から5、百の位にも1から5、十の位にも、一の位にも1から5を選ぶことができる。

これはすべてに1を選ぶこともできるし、選ばないこともできる。

他の数字に対しても同じことである。

このように、\( n \)個のものから、重複を許して、\( r \)個を取り出す順列を重複順列という。

図2.

問題に戻って、何通りあるのかを考えていく。すると、すべての位に5個選ぶことができて（図2）、 それは同時に起こるから積の法則より、

となり、625通りであることがわかる。

このように、\( n \)個から\( r \)個取る場合の重複順列の総数は

である。