円順列
カテゴリー:数学A
円順列について説明していこう。
\( n \)個の中から\( r \)を取る順列は、\( {}_n \mathrm{P}_r \)で総数が求められる。
この順列は\( n \)個の中から\( r \)を取り、一列に並べる場合の数の総数である。
では、取り出した\( r \)個を一列ではなく、円に並べた場合はどうなるだろう?
このように、いくつかのものを円形に並べた配列を円順列または、じゅず順列と呼ぶ。
異なる、\( n \)個のものを円形に並べた、円順列の総数の公式は、
\begin{align} \frac{{}_n \mathrm{P}_n}{n} = \frac{n!}{n} = (n-1)! \end{align}
で表される。
以下では、より詳細にこの公式を導いていく。
A, B, C, D, Eの5人が手をつないで輪を作る時の総数はいくつになるか?
このような問題があったとする。
もし、1列に並べる場合であれば、
\begin{align} 5! = 120 \end{align}
となり、120通りであることがわかる。
しかし、円順列では、回転させて一致する並び方は同じ並びであると考える。
これは、A, B, C, D, Eの場所は異なるものの、並び順はすべて同じだからである。
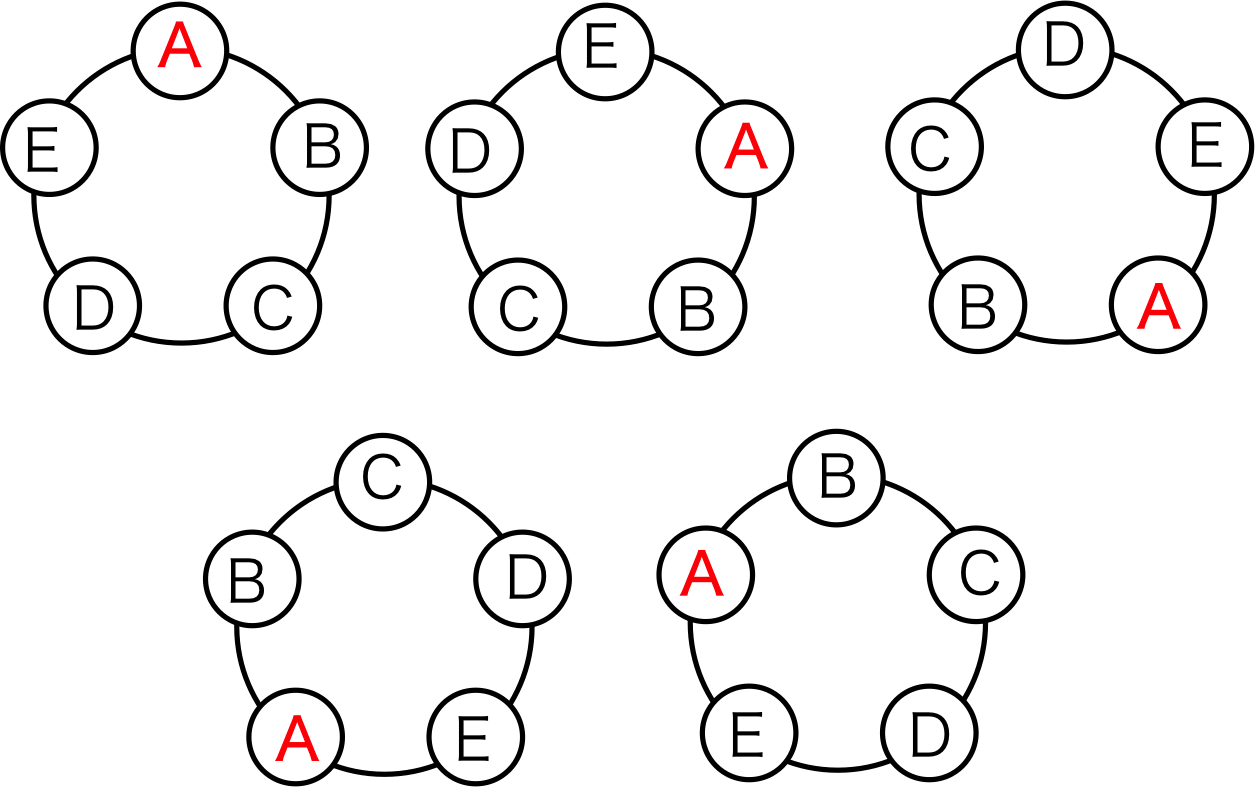
図1.すべて同じ並び方
つまり、一度輪を作ると、図1のように5通りの同じ輪ができることになる。
5通りの順列(120通り)に対して、重複する通り(5通り)を考えるので、
\begin{align} 120\div5=24 \end{align}
となり、24通りであることがわかる。
Aの位置を固定して考えた場合
残されたB、C、D、Eの並び方を考えると(5-1)!通りであることがわかる。
このことから、5人が手をつないで輪を作る並び方の求め方は
\begin{align} \frac{4!}{4} = 24 \end{align}
となる。
つまり、\( n \)個のもので円順列を作った場合、1つを固定して残りのものの順列を求めるので
\begin{align} \frac{n!}{n} = (n-1)! \end{align}
となるのである。
例題
父、母、兄、姉、私の5人家族が円卓に座る時、父と母が隣り合って座る並び方の総数はいくつ?
この問題の解を考える。
こういった隣り合うものを含む円順列の並び方の総数を求める場合は、図2のように「隣りあわなければならない人」を一括りにして考えるとわかりやすい。

図2.
この問題の場合は、「父と母が隣り合って座る並び方」なので、父と母をまとめて、「親」として考える。
すると、4人が円卓に座る並び方の総数として考えることができる。
さらに、父と母の座り方は\(2! \)通りあり、円卓に座る場合と同時に起きるので、積の法則により、4人の円順列の総数と掛け合わせることで
\begin{align} (4-1)! \times 2! = 12 \end{align}
となり、12通りあることがわかる。