順列

カテゴリー：数学A

ある集合の中からいくつかを選び、順序をつけて1列に並べる配列を順列という。

ではその並べ方をいくつ考えるのか例題を使って考えていこうと思う。

図1のようにA, B, C, Dの4人がいるとする。この4人の中から異なる3人を選んで1列に並べる配列（順列）は何通り考えられるだろうか？

図1.

まずは、樹形図を描く方法が簡単である。

図2にこの問題の樹形図を示す。

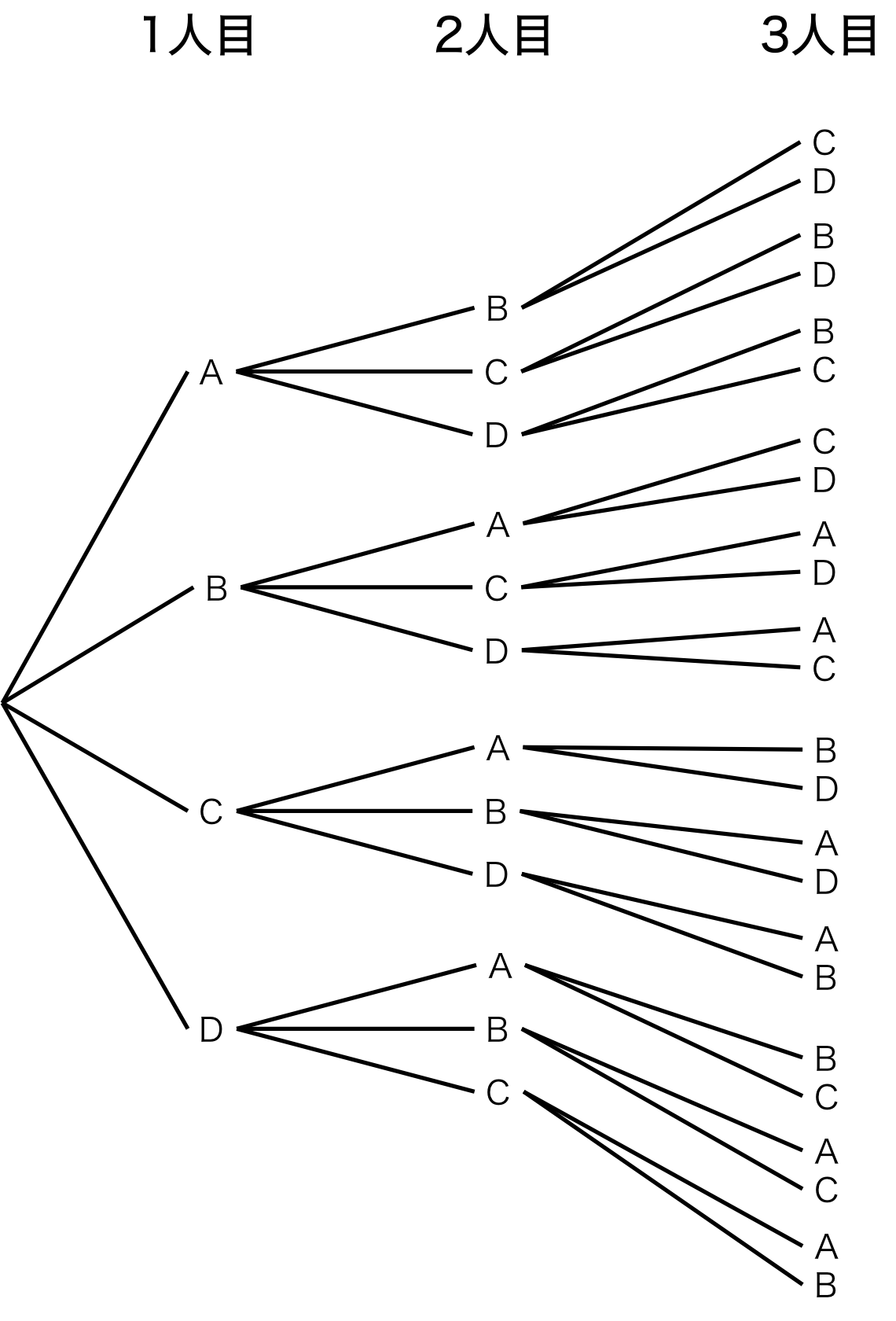
図2. A, B, C, Dから3人選んで並ぶ時の樹形図

このことからA, B, C, Dから異なる3人を選んで1列に並べる配列は24通りあることがわかる。

ではもっと詳しく見ていこう。

3人選ぶうちの1人目は、4人の中から1人選べばよいので4通り考えられる。

次に2人目は1人目を除いた3通り考えられる。

同じように3人目は1人目と2人目を除いた2通り考えられる。

この時、1人目、2人目、3人目を選ぶ事象は同時に起こる（1人目を選ばずに2人目は選べない）。

よって、積の法則より、4人から3人を選んで並べる配列は

から、24通りと求めることができるのである。

このように\( n \)個の中から\( r \)個を取り出して並べる順列は通常、

と表される。この時の、\( \mathrm{P} \)の読み方はパーミテーション（Permutation）で、英語の意味は「順列」である。

\( \mathrm{P} \)の計算方法

\( {}_n\mathrm{P}_r \)を数式として表すと、 \begin{eqnarray} {}_n\mathrm{P}_r = n \times (n-1) \times (n-2) \times (n-3) \times \cdots \times (n-r+1) \end{eqnarray}

となる。これだと分かりにくいので、図3で説明する。

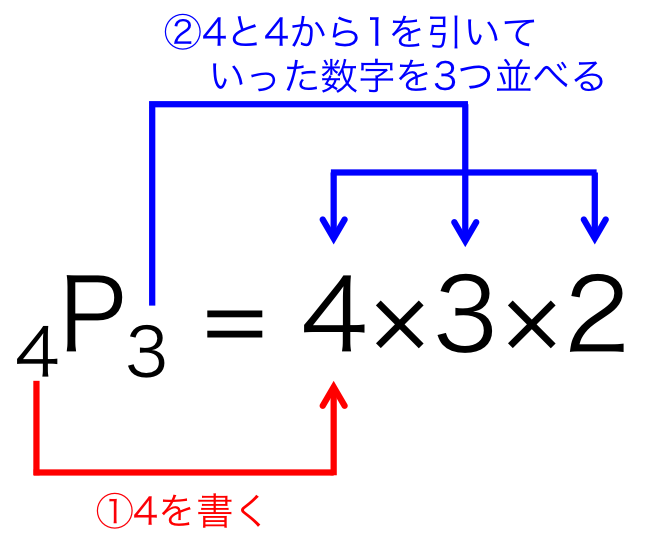
図3. Pの計算方法

Pの計算は、左下についている数字から掛け算を始める。

左下の数字から1を引いていった数字を掛け合わせていく。

何回掛け合わせるかというと、Pの右下についている数字の回数までである。

図3の例を使って説明してみると、4から掛け算を始めて、1を引いていった数字を4を含めて3回掛け合わせていく、 つまり、\( 4 \times 3 \times 2 \)となるのである。

これを使うと、もっと人数を増やして、A, B, C, D, E, Fの6人から5人を選んで一列に並べる配列は、

より、720通りあることがわかる。