和の法則

カテゴリー：数学A

大きいサイコロと小さいサイコロの2つのサイコロを同時に投げる時、それぞれの目の和が8または9になる場合は何通りあるだろうか？

まず、目の和が8になる事象のことを事象Aと呼ぶとする。

事象Aが起こる場合は下の表から、

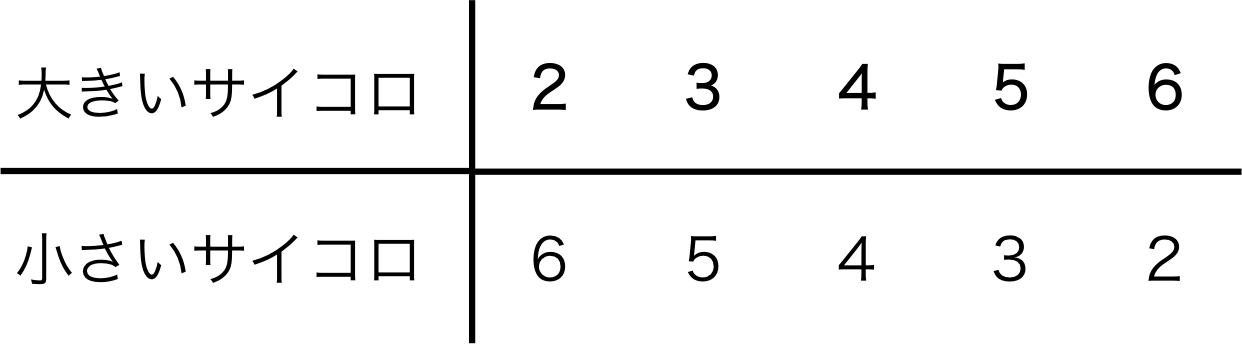
表1.　事象A（サイコロの目の和が8になる場合）

5通りであることがわかる。

次に、目の和が9になる事象のことを事象Bと呼ぶことにする。

事象Bが起こる場合は表2より、

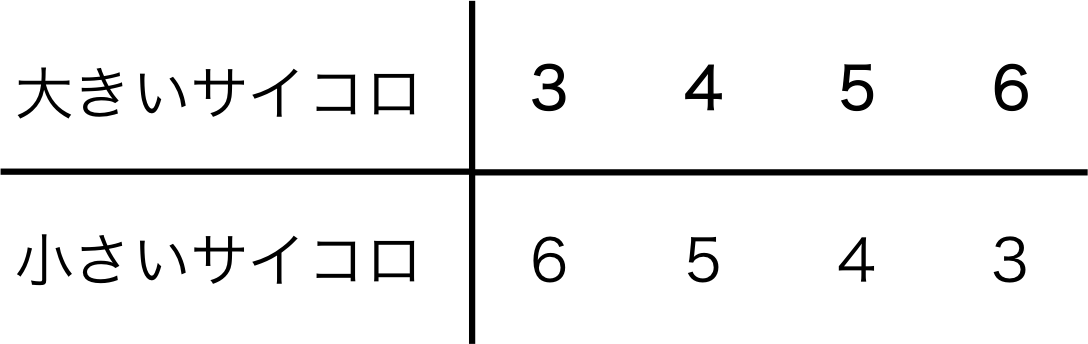
表2.　事象B（サイコロの目の和が9になる場合）

4通りである。

大小2つのサイコロを同時に振った場合、それぞれの目の和が8になることと、9になることは絶対に同時に起こらない。

つまり、目の和が8または9になる場合は

つまり、9通りである。

このように、同時に起こらない2つの事象A、 Bがあり、Aが\(n\)通り、Bが\(m\)通りの起こり方があるとすると、 AまたはBのどちらかが起こる場合は、\(n+m\)通りであると言うことが言える。

これを、和の法則と呼ぶ。

和の法則と積の法則の違い

和の法則と似た法則に積の法則がある。

こちらは、AとBが同時に起こる場合、何通りの起こり方があるのかを示す法則である。

この中で、和の法則はAとBの2つの事象があった時に、「AまたはBが起こる場合」と言うように、「または」という言葉を使って条件を表現できるのである。

積の法則は、「AかつB」と「かつ」を使って表される。

積の法則は別のページで紹介する。