パスカルの三角形

カテゴリー：数学A

二項定理により、\( (a+b)^n \)を展開した際の係数である二項係数を導出することができた。

二項係数\( {}_n\mathrm{C}_0,\ {}_n\mathrm{C}_1,\ {}_n\mathrm{C}_2,\ {}_n\mathrm{C}_3,\ \cdots,\ {}_n\mathrm{C}_n,\)を\(n=1,\ 2,\ 3,\ 4,\ 5\)の順で書くと図1のようになる。

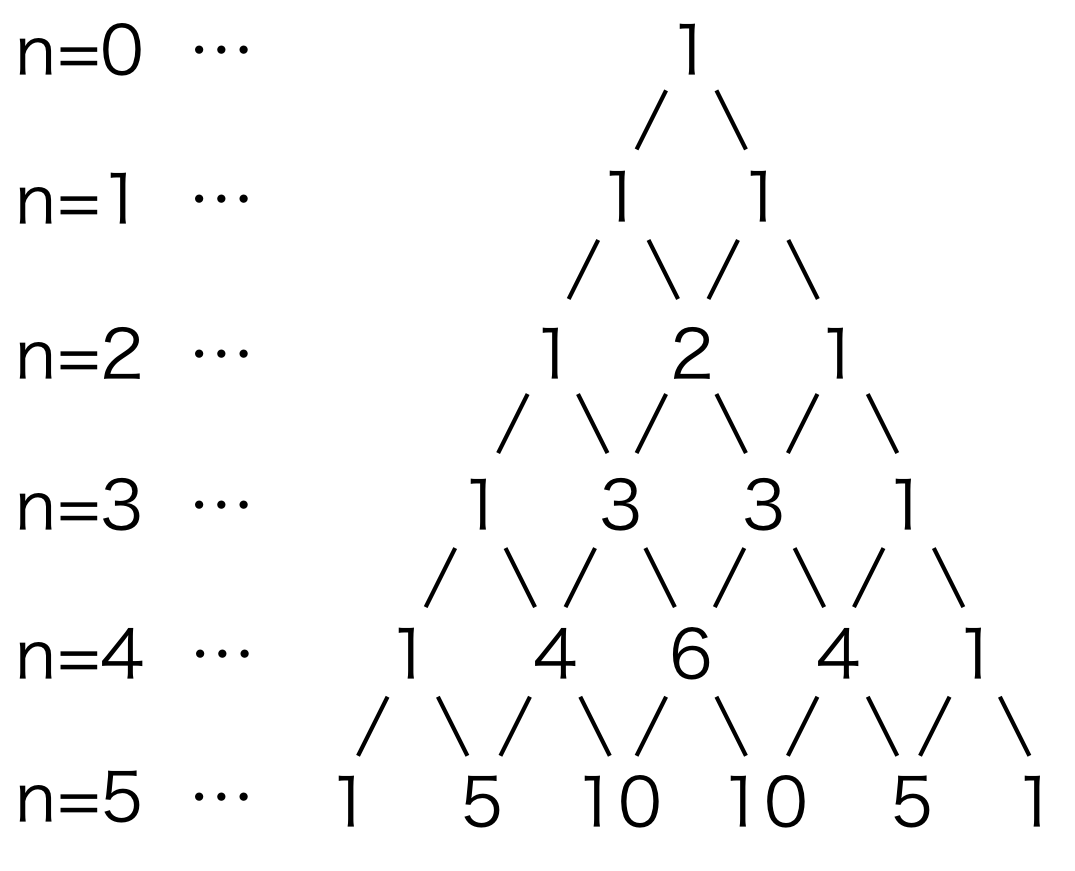
図1.　パスカルの三角形

これをパスカルの三角形と呼ぶ。

パスカルの三角形は以下の3つの規則から成り立っており、\(n\)の値が10以下ほどであれば簡単に作ることができる。

　　1.　各行の左右の端は1である。
　　2.　両端以外の数字は左上と右上の数字を足した値である。
　　3.　左右対象である。

　

パスカルの三角形を使うことで、二項定理より比較的容易に二項係数を求めることができる。