同じものを含む順列：道順（最短経路）

カテゴリー：数学A

ここでは同じものを含む順列の中でよく出題される問題を解いて行く。

図1の上図のように、東西に5本、南北に6本の碁盤目状の道があるとする。この時、PからQまで最短で行く道順は何通りあるだろうか。

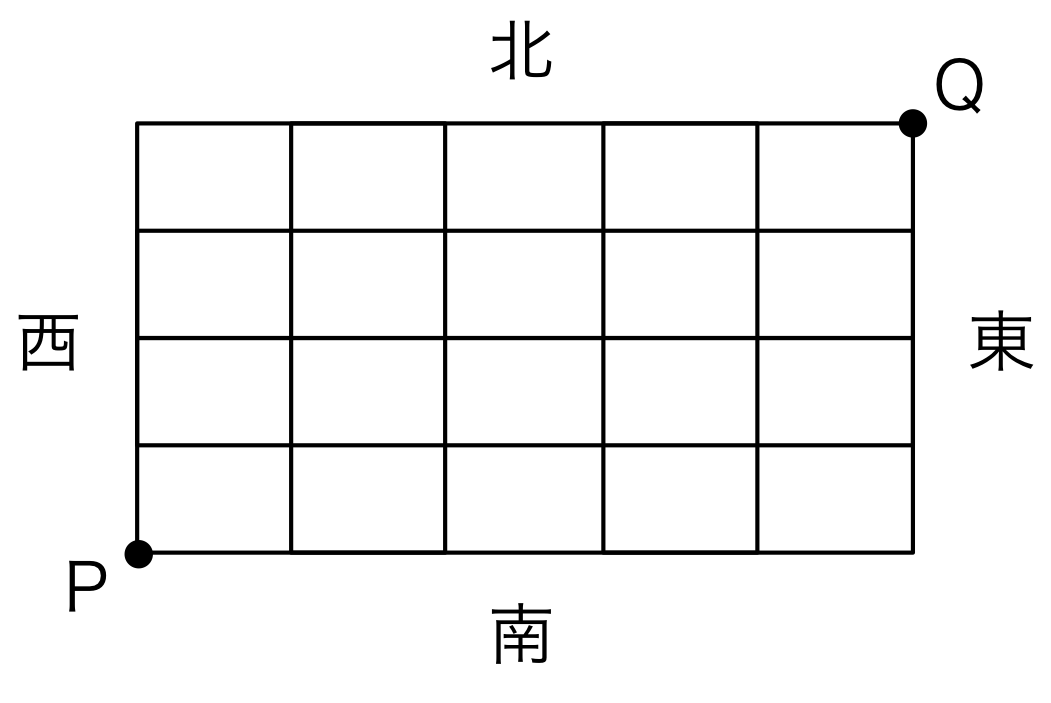
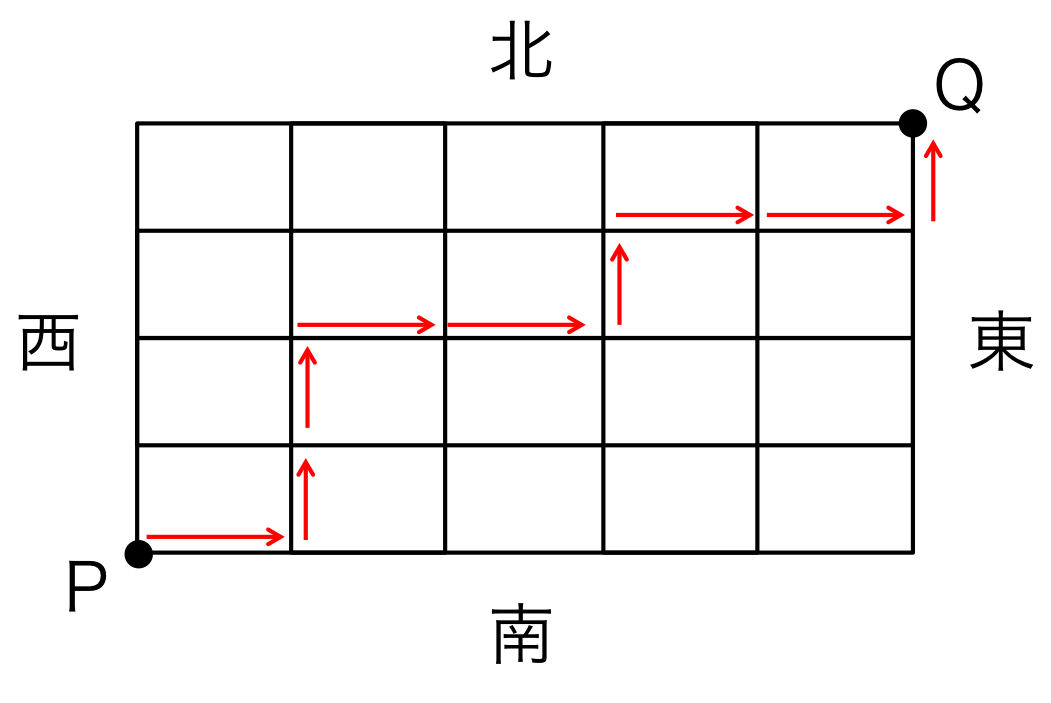
図2.

最短でPからQに向かうので、進む方向は必ず北方向（上向き矢印）か東方向（右向き矢印）である。

図1の下の図のような道順が考えられるのである。

この時、道順である矢印だけを抜き出して考えると図3のようになる。

図3.

つまり、PからQまで行く最短の方法は上向きの矢印が4つ、右向きの矢印が5つであることがわかる。

このことからPからQまで行く最短の方法は、これらの矢印を1列に並べる総数に等しいのである。

これは同じものを含む順列であるので、

となり、126通りあることがわかるのである。